
Question Number 130852 by Algoritm last updated on 29/Jan/21
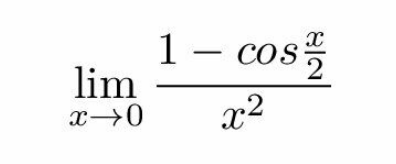
Answered by Dwaipayan Shikari last updated on 29/Jan/21
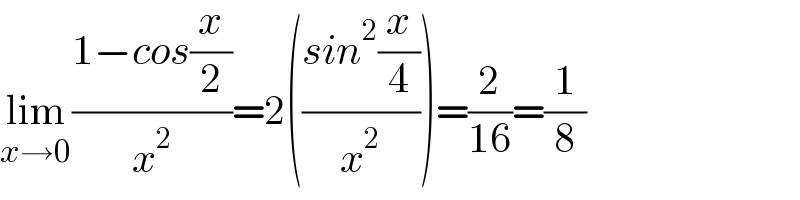
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−{cos}\frac{{x}}{\mathrm{2}}}{{x}^{\mathrm{2}} }=\mathrm{2}\left(\frac{{sin}^{\mathrm{2}} \frac{{x}}{\mathrm{4}}}{{x}^{\mathrm{2}} }\right)=\frac{\mathrm{2}}{\mathrm{16}}=\frac{\mathrm{1}}{\mathrm{8}} \\ $$
Answered by benjo_mathlover last updated on 30/Jan/21
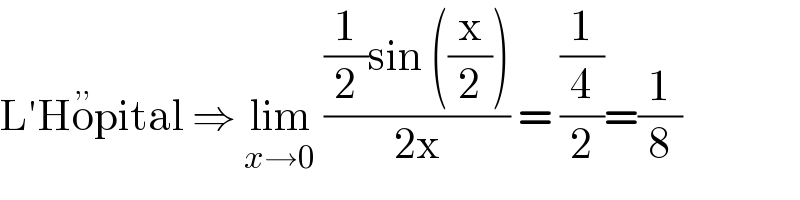
$$\mathrm{L}'\mathrm{H}\overset{,,} {\mathrm{o}pital}\:\Rightarrow\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\left(\frac{\mathrm{x}}{\mathrm{2}}\right)}{\mathrm{2x}}\:=\:\frac{\frac{\mathrm{1}}{\mathrm{4}}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{8}} \\ $$
Answered by malwan last updated on 30/Jan/21
![lim_(x→0) ((1−[1−((((x/2))^2 )/(2!)) + ((((x/2))^4 )/(4!)) −...])/x^2 ) = ((((1/4)))/(2×1)) = (1/8)](Q130879.png)
$$\underset{{x}\rightarrow\mathrm{0}} {{lim}}\:\frac{\mathrm{1}−\left[\mathrm{1}−\frac{\left(\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{2}!}\:+\:\frac{\left(\frac{{x}}{\mathrm{2}}\right)^{\mathrm{4}} }{\mathrm{4}!}\:−...\right]}{{x}^{\mathrm{2}} } \\ $$$$=\:\frac{\left(\frac{\mathrm{1}}{\mathrm{4}}\right)}{\mathrm{2}×\mathrm{1}}\:=\:\frac{\mathrm{1}}{\mathrm{8}} \\ $$
Answered by malwan last updated on 30/Jan/21
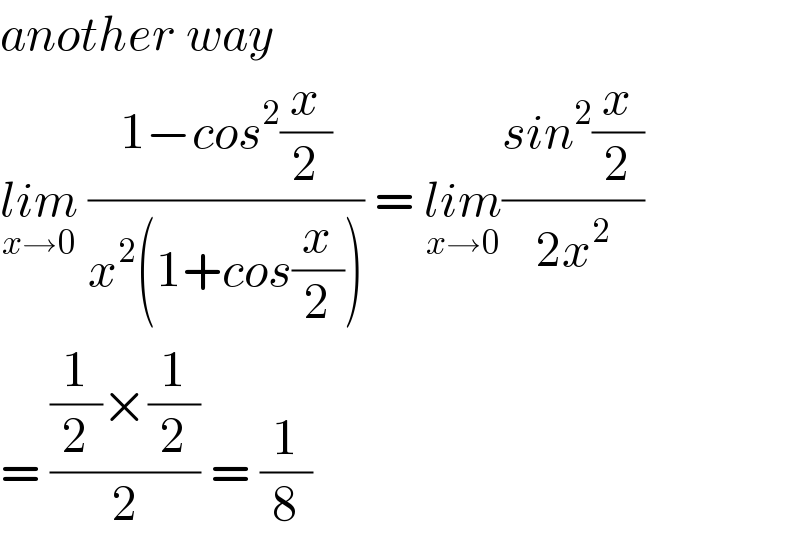
$${another}\:{way} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {{lim}}\:\frac{\mathrm{1}−{cos}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{{x}^{\mathrm{2}} \left(\mathrm{1}+{cos}\frac{{x}}{\mathrm{2}}\right)}\:=\:\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{{sin}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{\mathrm{2}{x}^{\mathrm{2}} } \\ $$$$=\:\frac{\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{2}}\:=\:\frac{\mathrm{1}}{\mathrm{8}} \\ $$
Answered by malwan last updated on 30/Jan/21
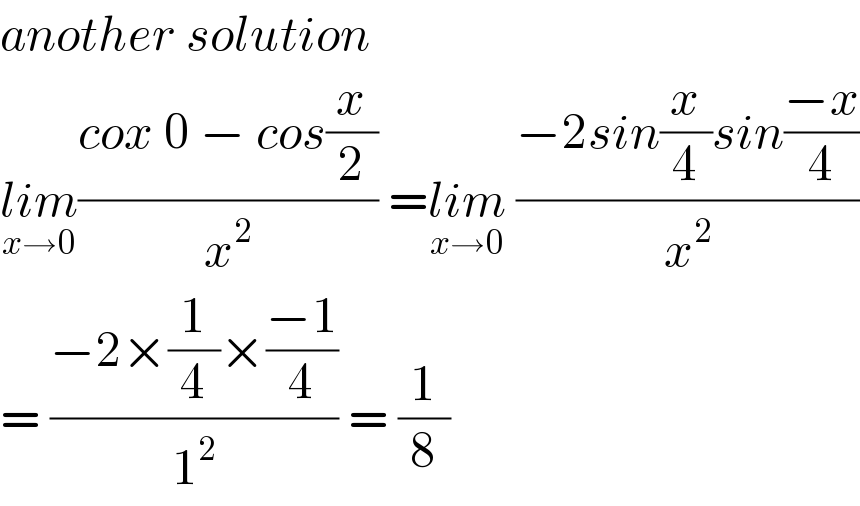
$${another}\:{solution} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{{cox}\:\mathrm{0}\:−\:{cos}\frac{{x}}{\mathrm{2}}}{{x}^{\mathrm{2}} }\:=\underset{{x}\rightarrow\mathrm{0}} {{lim}}\:\frac{−\mathrm{2}{sin}\frac{{x}}{\mathrm{4}}{sin}\frac{−{x}}{\mathrm{4}}}{{x}^{\mathrm{2}} } \\ $$$$=\:\frac{−\mathrm{2}×\frac{\mathrm{1}}{\mathrm{4}}×\frac{−\mathrm{1}}{\mathrm{4}}}{\mathrm{1}^{\mathrm{2}} }\:=\:\frac{\mathrm{1}}{\mathrm{8}} \\ $$
