Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 130753 by Algoritm last updated on 28/Jan/21

Answered by Dwaipayan Shikari last updated on 28/Jan/21

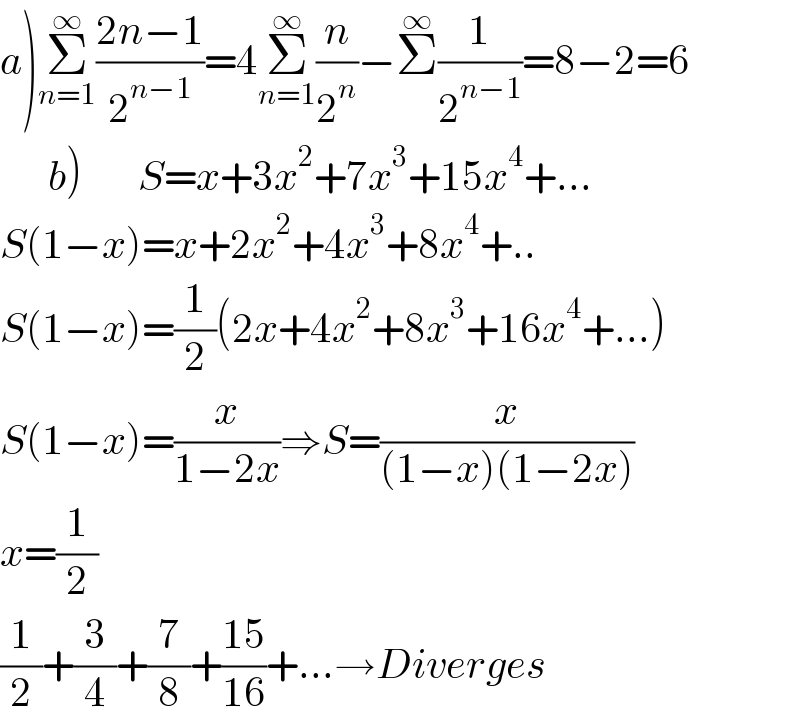
a)Σ_(n=1) ^∞ ((2n−1)/2^(n−1) )=4Σ_(n=1) ^∞ (n/2^n )−Σ^∞ (1/2^(n−1) )=8−2=6 b) S=x+3x^2 +7x^3 +15x^4 +... S(1−x)=x+2x^2 +4x^3 +8x^4 +.. S(1−x)=(1/2)(2x+4x^2 +8x^3 +16x^4 +...) S(1−x)=(x/(1−2x))⇒S=(x/((1−x)(1−2x))) x=(1/2) (1/2)+(3/4)+(7/8)+((15)/(16))+...→Diverges

$$\left.{a}\right)\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{2}{n}−\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{1}} }=\mathrm{4}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}}{\mathrm{2}^{{n}} }−\overset{\infty} {\sum}\frac{\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{1}} }=\mathrm{8}−\mathrm{2}=\mathrm{6} \\ $$$$\left.\:\:\:\:\:\:{b}\right)\:\:\:\:\:\:\:{S}={x}+\mathrm{3}{x}^{\mathrm{2}} +\mathrm{7}{x}^{\mathrm{3}} +\mathrm{15}{x}^{\mathrm{4}} +... \\ $$$${S}\left(\mathrm{1}−{x}\right)={x}+\mathrm{2}{x}^{\mathrm{2}} +\mathrm{4}{x}^{\mathrm{3}} +\mathrm{8}{x}^{\mathrm{4}} +.. \\ $$$${S}\left(\mathrm{1}−{x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}{x}+\mathrm{4}{x}^{\mathrm{2}} +\mathrm{8}{x}^{\mathrm{3}} +\mathrm{16}{x}^{\mathrm{4}} +...\right) \\ $$$${S}\left(\mathrm{1}−{x}\right)=\frac{{x}}{\mathrm{1}−\mathrm{2}{x}}\Rightarrow{S}=\frac{{x}}{\left(\mathrm{1}−{x}\right)\left(\mathrm{1}−\mathrm{2}{x}\right)} \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\: \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{7}}{\mathrm{8}}+\frac{\mathrm{15}}{\mathrm{16}}+...\rightarrow{Diverges} \\ $$

Answered by JDamian last updated on 28/Jan/21

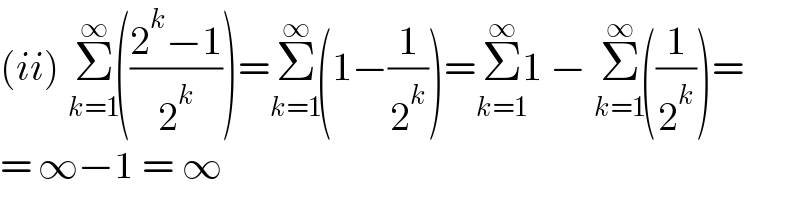
(ii) Σ_(k=1) ^(∞) (((2^k −1)/2^k ))=Σ_(k=1) ^(∞) (1−(1/2^k ))=Σ_(k=1) ^(∞) 1 − Σ_(k=1) ^(∞) ((1/2^k ))= = ∞−1 = ∞

$$\left({ii}\right)\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\Sigma}}\left(\frac{\mathrm{2}^{{k}} −\mathrm{1}}{\mathrm{2}^{{k}} }\right)=\underset{{k}=\mathrm{1}} {\overset{\infty} {\Sigma}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{{k}} }\right)=\underset{{k}=\mathrm{1}} {\overset{\infty} {\Sigma}}\mathrm{1}\:−\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\Sigma}}\left(\frac{\mathrm{1}}{\mathrm{2}^{{k}} }\right)= \\ $$$$=\:\infty−\mathrm{1}\:=\:\infty \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com