
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 130634 by EDWIN88 last updated on 27/Jan/21

Answered by liberty last updated on 27/Jan/21
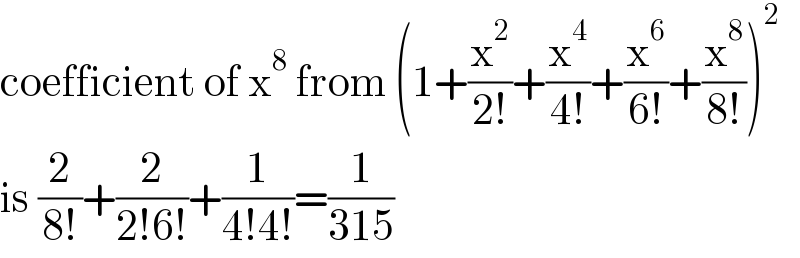
$$\mathrm{coefficient}\:\mathrm{of}\:\mathrm{x}^{\mathrm{8}} \:\mathrm{from}\:\left(\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{4}!}+\frac{\mathrm{x}^{\mathrm{6}} }{\mathrm{6}!}+\frac{\mathrm{x}^{\mathrm{8}} }{\mathrm{8}!}\right)^{\mathrm{2}} \\ $$$$\mathrm{is}\:\frac{\mathrm{2}}{\mathrm{8}!}+\frac{\mathrm{2}}{\mathrm{2}!\mathrm{6}!}+\frac{\mathrm{1}}{\mathrm{4}!\mathrm{4}!}=\frac{\mathrm{1}}{\mathrm{315}} \\ $$
