
Question Number 130476 by shaker last updated on 26/Jan/21

Answered by TheSupreme last updated on 26/Jan/21
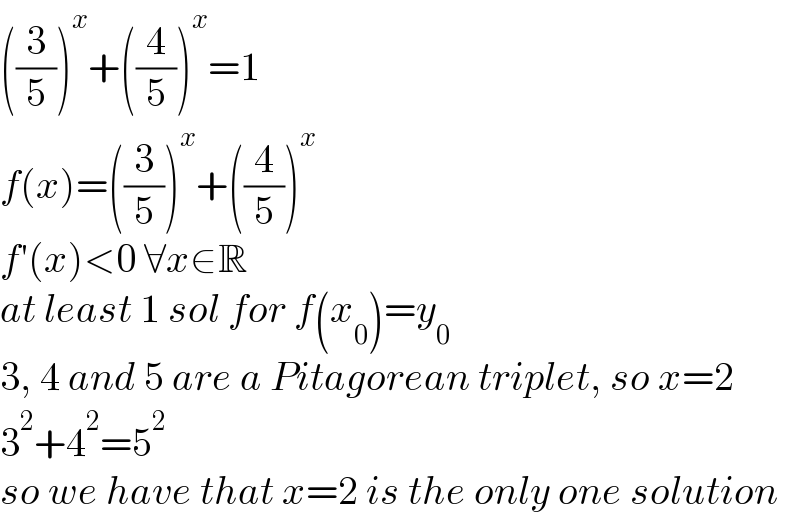
$$\left(\frac{\mathrm{3}}{\mathrm{5}}\right)^{{x}} +\left(\frac{\mathrm{4}}{\mathrm{5}}\right)^{{x}} =\mathrm{1} \\ $$$${f}\left({x}\right)=\left(\frac{\mathrm{3}}{\mathrm{5}}\right)^{{x}} +\left(\frac{\mathrm{4}}{\mathrm{5}}\right)^{{x}} \\ $$$${f}'\left({x}\right)<\mathrm{0}\:\forall{x}\in\mathbb{R} \\ $$$${at}\:{least}\:\mathrm{1}\:{sol}\:{for}\:{f}\left({x}_{\mathrm{0}} \right)={y}_{\mathrm{0}} \\ $$$$\mathrm{3},\:\mathrm{4}\:{and}\:\mathrm{5}\:{are}\:{a}\:{Pitagorean}\:{triplet},\:{so}\:{x}=\mathrm{2} \\ $$$$\mathrm{3}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} =\mathrm{5}^{\mathrm{2}} \\ $$$${so}\:{we}\:{have}\:{that}\:{x}=\mathrm{2}\:{is}\:{the}\:{only}\:{one}\:{solution} \\ $$
