
Question Number 130358 by ajfour last updated on 24/Jan/21
Commented by ajfour last updated on 24/Jan/21
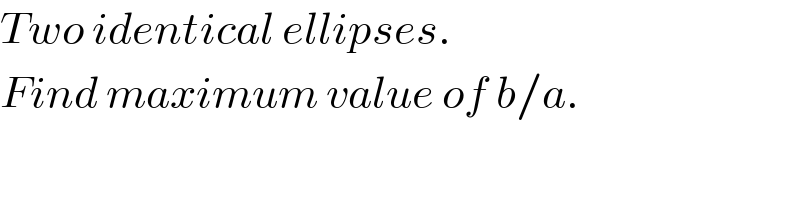
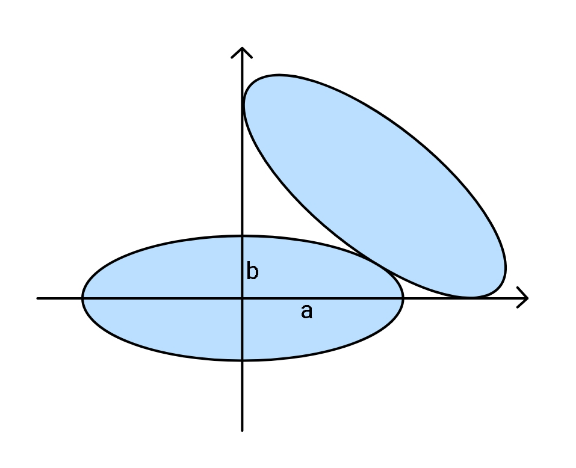
$${Two}\:{identical}\:{ellipses}. \\ $$$${Find}\:{maximum}\:{value}\:{of}\:{b}/{a}. \\ $$
Commented by MJS_new last updated on 25/Jan/21
![once again thinking backwards (exchanging the ellipses) let a=1 (1) search 2 tangents to the 1^(st) ellipse with t_1 ⊥t_2 (2) shift and rotate the ellipse to get the 2^(nd) ellipse with center at t_1 ∩t_2 and axes t_1 and t_2 [the intersections of all possible rectangular pairs of tangents form a circle with radius (√(b^2 +1)) and center ((0),(0) ) ] I think we get the maximum b when t_1 and t_2 are symmetric to x=0 ⇔ t_1 ∩t_2 = ((0),((√(b^2 +1))) ) in this case the equation of the 2^(nd) ellipse is easy to get because the angle of rotation is (π/4). now we must intersect the ellipses and find b in order to get exactly one intersection. this leads to a 4^(th) degree polynome for x. I once posted the conditions for all possible kinds of solutions for this. it leads to a 12^(th) degree polynome for b^2 which has exactly one real solution we can only approximate. I get b≈.368 671 126 255 not sure if my idea is right... but it looks a lot to me we will get a smaller value for b when using a different pair of tangents...](Q130403.png)
$$\mathrm{once}\:\mathrm{again}\:\mathrm{thinking}\:\mathrm{backwards}\:\left(\mathrm{exchanging}\right. \\ $$$$\left.\mathrm{the}\:\mathrm{ellipses}\right) \\ $$$$\mathrm{let}\:{a}=\mathrm{1} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{search}\:\mathrm{2}\:\mathrm{tangents}\:\mathrm{to}\:\mathrm{the}\:\mathrm{1}^{\mathrm{st}} \:\mathrm{ellipse}\:\mathrm{with} \\ $$$$\:\:\:\:\:\:\:{t}_{\mathrm{1}} \bot{t}_{\mathrm{2}} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{shift}\:\mathrm{and}\:\mathrm{rotate}\:\mathrm{the}\:\mathrm{ellipse}\:\mathrm{to}\:\mathrm{get}\:\mathrm{the}\:\mathrm{2}^{\mathrm{nd}} \\ $$$$\:\:\:\:\:\:\:\mathrm{ellipse}\:\mathrm{with}\:\mathrm{center}\:\mathrm{at}\:{t}_{\mathrm{1}} \cap{t}_{\mathrm{2}} \:\mathrm{and}\:\mathrm{axes}\:{t}_{\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\mathrm{and}\:{t}_{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\left[\mathrm{the}\:\mathrm{intersections}\:\mathrm{of}\:\mathrm{all}\:\mathrm{possible}\:\mathrm{rectangular}\right. \\ $$$$\:\:\:\:\:\:\:\:\mathrm{pairs}\:\mathrm{of}\:\mathrm{tangents}\:\mathrm{form}\:\mathrm{a}\:\mathrm{circle}\:\mathrm{with}\:\mathrm{radius} \\ $$$$\left.\:\:\:\:\:\:\:\:\sqrt{{b}^{\mathrm{2}} +\mathrm{1}}\:\mathrm{and}\:\mathrm{center}\:\begin{pmatrix}{\mathrm{0}}\\{\mathrm{0}}\end{pmatrix}\:\right] \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{we}\:\mathrm{get}\:\mathrm{the}\:\mathrm{maximum}\:{b}\:\mathrm{when}\:{t}_{\mathrm{1}} \:\mathrm{and} \\ $$$${t}_{\mathrm{2}} \:\mathrm{are}\:\mathrm{symmetric}\:\mathrm{to}\:{x}=\mathrm{0}\:\Leftrightarrow\:{t}_{\mathrm{1}} \cap{t}_{\mathrm{2}} =\begin{pmatrix}{\mathrm{0}}\\{\sqrt{{b}^{\mathrm{2}} +\mathrm{1}}}\end{pmatrix} \\ $$$$\mathrm{in}\:\mathrm{this}\:\mathrm{case}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{the}\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{ellipse}\:\mathrm{is} \\ $$$$\mathrm{easy}\:\mathrm{to}\:\mathrm{get}\:\mathrm{because}\:\mathrm{the}\:\mathrm{angle}\:\mathrm{of}\:\mathrm{rotation}\:\mathrm{is} \\ $$$$\frac{\pi}{\mathrm{4}}.\:\mathrm{now}\:\mathrm{we}\:\mathrm{must}\:\mathrm{intersect}\:\mathrm{the}\:\mathrm{ellipses}\:\mathrm{and} \\ $$$$\mathrm{find}\:{b}\:\mathrm{in}\:\mathrm{order}\:\mathrm{to}\:\mathrm{get}\:\mathrm{exactly}\:\mathrm{one}\:\mathrm{intersection}. \\ $$$$\mathrm{this}\:\mathrm{leads}\:\mathrm{to}\:\mathrm{a}\:\mathrm{4}^{\mathrm{th}} \:\mathrm{degree}\:\mathrm{polynome}\:\mathrm{for}\:{x}. \\ $$$$\mathrm{I}\:\mathrm{once}\:\mathrm{posted}\:\mathrm{the}\:\mathrm{conditions}\:\mathrm{for}\:\mathrm{all}\:\mathrm{possible} \\ $$$$\mathrm{kinds}\:\mathrm{of}\:\mathrm{solutions}\:\mathrm{for}\:\mathrm{this}.\:\mathrm{it}\:\mathrm{leads}\:\mathrm{to}\:\mathrm{a}\:\mathrm{12}^{\mathrm{th}} \\ $$$$\mathrm{degree}\:\mathrm{polynome}\:\mathrm{for}\:{b}^{\mathrm{2}} \:\mathrm{which}\:\mathrm{has}\:\mathrm{exactly} \\ $$$$\mathrm{one}\:\mathrm{real}\:\mathrm{solution}\:\mathrm{we}\:\mathrm{can}\:\mathrm{only}\:\mathrm{approximate}. \\ $$$$\mathrm{I}\:\mathrm{get}\:{b}\approx.\mathrm{368}\:\mathrm{671}\:\mathrm{126}\:\mathrm{255} \\ $$$$ \\ $$$$\mathrm{not}\:\mathrm{sure}\:\mathrm{if}\:\mathrm{my}\:\mathrm{idea}\:\mathrm{is}\:\mathrm{right}...\:\mathrm{but}\:\mathrm{it}\:\mathrm{looks}\:\mathrm{a} \\ $$$$\mathrm{lot}\:\mathrm{to}\:\mathrm{me}\:\mathrm{we}\:\mathrm{will}\:\mathrm{get}\:\mathrm{a}\:\mathrm{smaller}\:\mathrm{value}\:\mathrm{for}\:{b}\:\mathrm{when} \\ $$$$\mathrm{using}\:\mathrm{a}\:\mathrm{different}\:\mathrm{pair}\:\mathrm{of}\:\mathrm{tangents}... \\ $$
Commented by MJS_new last updated on 25/Jan/21
![the equations for plotting are: ellipse 1: y=±b(√(1−x^2 )) tangents: y=±x+(√(b^2 +1)) ellipse 2: y=((1−b^2 )/(b^2 +1))x+(√(b^2 +1))±((b(√(2b^2 +2−4x^2 )))/(b^2 +1)) it seems obvious that (1) if b gets smaller the ellipses will lose contact ⇒ we have to rotate the tangents (2) if b gets larger we get 2 intersections ⇒ we have to rotate the tangents but then the space gets even smaller [this needs a proof...]](Q130404.png)
$$\mathrm{the}\:\mathrm{equations}\:\mathrm{for}\:\mathrm{plotting}\:\mathrm{are}: \\ $$$$\mathrm{ellipse}\:\mathrm{1}:\:\:\:\:{y}=\pm{b}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$$\mathrm{tangents}:\:\:{y}=\pm{x}+\sqrt{{b}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\mathrm{ellipse}\:\mathrm{2}:\:\:\:\:{y}=\frac{\mathrm{1}−{b}^{\mathrm{2}} }{{b}^{\mathrm{2}} +\mathrm{1}}{x}+\sqrt{{b}^{\mathrm{2}} +\mathrm{1}}\pm\frac{{b}\sqrt{\mathrm{2}{b}^{\mathrm{2}} +\mathrm{2}−\mathrm{4}{x}^{\mathrm{2}} }}{{b}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\mathrm{it}\:\mathrm{seems}\:\mathrm{obvious}\:\mathrm{that} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{if}\:{b}\:\mathrm{gets}\:\mathrm{smaller}\:\mathrm{the}\:\mathrm{ellipses}\:\mathrm{will}\:\mathrm{lose}\:\mathrm{contact} \\ $$$$\:\:\:\:\:\Rightarrow\:\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{rotate}\:\mathrm{the}\:\mathrm{tangents} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{if}\:{b}\:\mathrm{gets}\:\mathrm{larger}\:\mathrm{we}\:\mathrm{get}\:\mathrm{2}\:\mathrm{intersections} \\ $$$$\:\:\:\:\:\Rightarrow\:\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{rotate}\:\mathrm{the}\:\mathrm{tangents}\:\mathrm{but}\:\mathrm{then} \\ $$$$\:\:\:\:\:\mathrm{the}\:\mathrm{space}\:\mathrm{gets}\:\mathrm{even}\:\mathrm{smaller} \\ $$$$\:\:\:\:\:\left[\mathrm{this}\:\mathrm{needs}\:\mathrm{a}\:\mathrm{proof}...\right] \\ $$
Commented by MJS_new last updated on 25/Jan/21
![above (1) obviously we rotate to the left ⇒ (2) we cannot rotate to the left with larger b but rotating to the right seems no good idea either [plot it!]](Q130405.png)
$$\mathrm{above}\:\left(\mathrm{1}\right)\:\mathrm{obviously}\:\mathrm{we}\:\mathrm{rotate}\:\mathrm{to}\:\mathrm{the}\:\mathrm{left} \\ $$$$\Rightarrow\:\left(\mathrm{2}\right)\:\mathrm{we}\:\mathrm{cannot}\:\mathrm{rotate}\:\mathrm{to}\:\mathrm{the}\:\mathrm{left}\:\mathrm{with} \\ $$$$\mathrm{larger}\:{b}\:\mathrm{but}\:\mathrm{rotating}\:\mathrm{to}\:\mathrm{the}\:\mathrm{right}\:\mathrm{seems}\:\mathrm{no} \\ $$$$\mathrm{good}\:\mathrm{idea}\:\mathrm{either}\:\left[\mathrm{plot}\:\mathrm{it}!\right] \\ $$
Commented by mr W last updated on 25/Jan/21
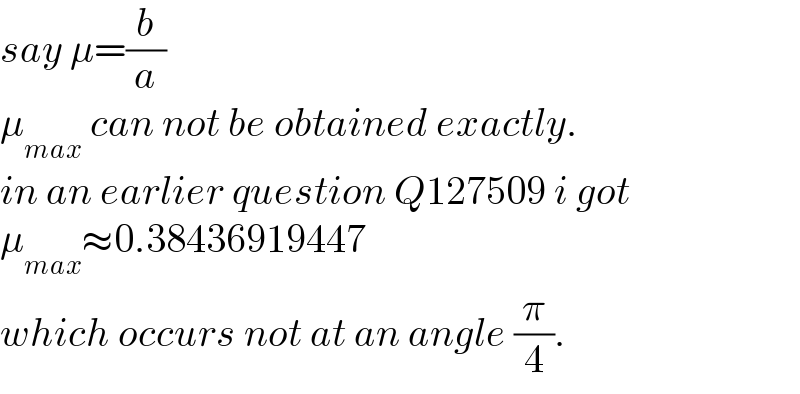
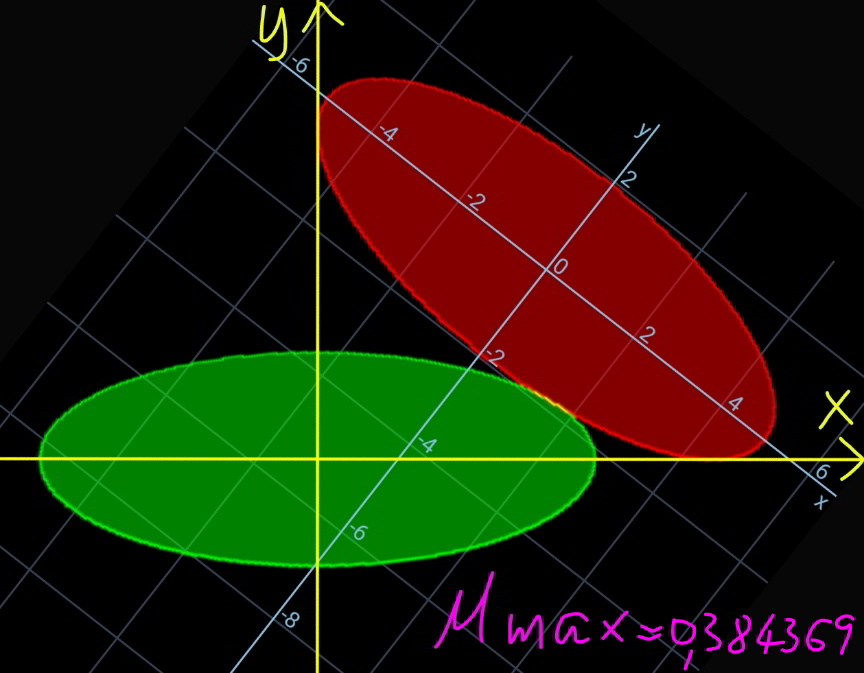
$${say}\:\mu=\frac{{b}}{{a}} \\ $$$$\mu_{{max}} \:{can}\:{not}\:{be}\:{obtained}\:{exactly}. \\ $$$${in}\:{an}\:{earlier}\:{question}\:{Q}\mathrm{127509}\:{i}\:{got} \\ $$$$\mu_{{max}} \approx\mathrm{0}.\mathrm{38436919447} \\ $$$${which}\:{occurs}\:{not}\:{at}\:{an}\:{angle}\:\frac{\pi}{\mathrm{4}}. \\ $$
Commented by mr W last updated on 25/Jan/21
Commented by MJS_new last updated on 25/Jan/21
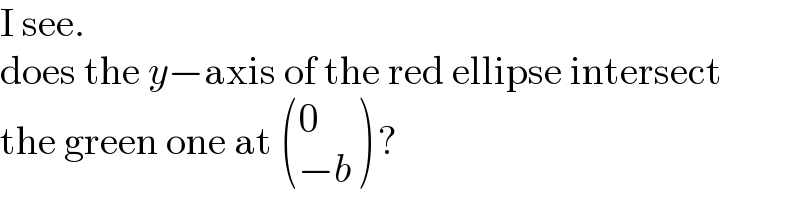
$$\mathrm{I}\:\mathrm{see}. \\ $$$$\mathrm{does}\:\mathrm{the}\:{y}−\mathrm{axis}\:\mathrm{of}\:\mathrm{the}\:\mathrm{red}\:\mathrm{ellipse}\:\mathrm{intersect} \\ $$$$\mathrm{the}\:\mathrm{green}\:\mathrm{one}\:\mathrm{at}\:\begin{pmatrix}{\mathrm{0}}\\{−{b}}\end{pmatrix}\:? \\ $$
Commented by mr W last updated on 25/Jan/21
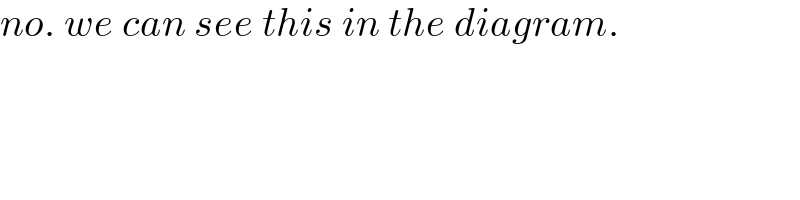
$${no}.\:{we}\:{can}\:{see}\:{this}\:{in}\:{the}\:{diagram}. \\ $$
