
Previous in Differential Equation Next in Differential Equation
Question Number 130301 by sarahvalencia last updated on 24/Jan/21

Answered by benjo_mathlover last updated on 24/Jan/21
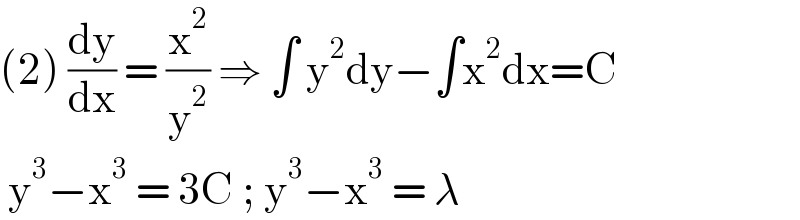
$$\left(\mathrm{2}\right)\:\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{y}^{\mathrm{2}} }\:\Rightarrow\:\int\:\mathrm{y}^{\mathrm{2}} \mathrm{dy}−\int\mathrm{x}^{\mathrm{2}} \mathrm{dx}=\mathrm{C} \\ $$$$\:\mathrm{y}^{\mathrm{3}} −\mathrm{x}^{\mathrm{3}} \:=\:\mathrm{3C}\:;\:\mathrm{y}^{\mathrm{3}} −\mathrm{x}^{\mathrm{3}} \:=\:\lambda\: \\ $$
Commented by benjo_mathlover last updated on 24/Jan/21
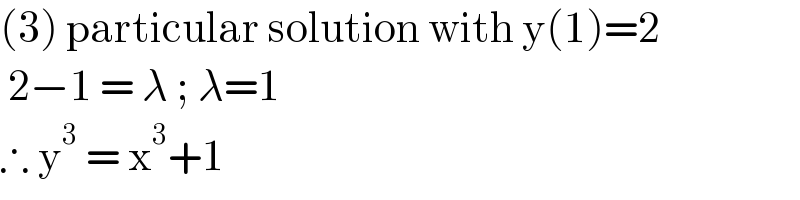
$$\left(\mathrm{3}\right)\:\mathrm{particular}\:\mathrm{solution}\:\mathrm{with}\:\mathrm{y}\left(\mathrm{1}\right)=\mathrm{2} \\ $$$$\:\mathrm{2}−\mathrm{1}\:=\:\lambda\:;\:\lambda=\mathrm{1} \\ $$$$\therefore\:\mathrm{y}^{\mathrm{3}} \:=\:\mathrm{x}^{\mathrm{3}} +\mathrm{1}\: \\ $$
