Question and Answers Forum

All Questions      Topic List

Coordinate Geometry Questions

Previous in All Question      Next in All Question      

Previous in Coordinate Geometry      Next in Coordinate Geometry      

Question Number 130263 by pete last updated on 23/Jan/21

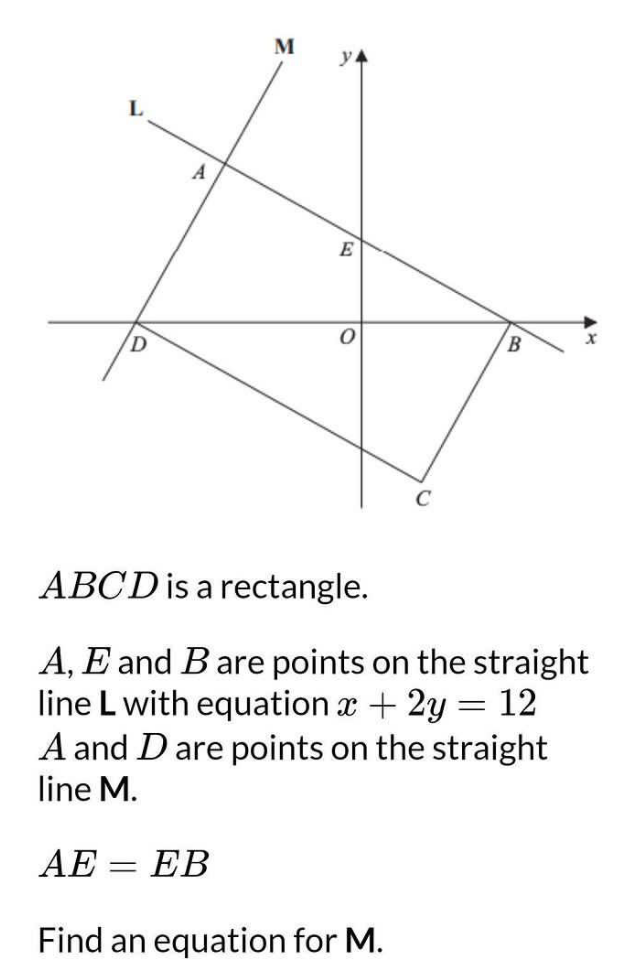
Answered by Olaf last updated on 23/Jan/21

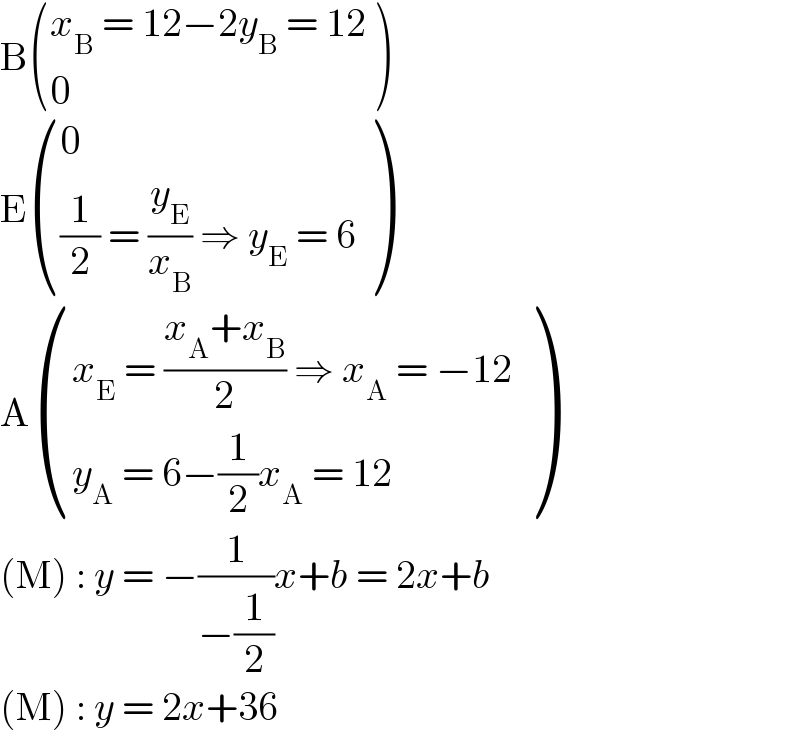
B (((x_B = 12−2y_B = 12)),(0) ) E ((0),(((1/2) = (y_E /x_B ) ⇒ y_E = 6)) ) A (((x_E = ((x_A +x_B )/2) ⇒ x_A = −12)),((y_A = 6−(1/2)x_A = 12 )) ) (M) : y = −(1/(−(1/2)))x+b = 2x+b (M) : y = 2x+36

$$\mathrm{B}\begin{pmatrix}{{x}_{\mathrm{B}} \:=\:\mathrm{12}−\mathrm{2}{y}_{\mathrm{B}} \:=\:\mathrm{12}}\\{\mathrm{0}}\end{pmatrix} \\ $$$$\mathrm{E}\begin{pmatrix}{\mathrm{0}}\\{\frac{\mathrm{1}}{\mathrm{2}}\:=\:\frac{{y}_{\mathrm{E}} }{{x}_{\mathrm{B}} }\:\Rightarrow\:{y}_{\mathrm{E}} \:=\:\mathrm{6}}\end{pmatrix} \\ $$$$\mathrm{A}\begin{pmatrix}{{x}_{\mathrm{E}} \:=\:\frac{{x}_{\mathrm{A}} +{x}_{\mathrm{B}} }{\mathrm{2}}\:\Rightarrow\:{x}_{\mathrm{A}} \:=\:−\mathrm{12}}\\{{y}_{\mathrm{A}} \:=\:\mathrm{6}−\frac{\mathrm{1}}{\mathrm{2}}{x}_{\mathrm{A}} \:=\:\mathrm{12}\:}\end{pmatrix} \\ $$$$\left(\mathrm{M}\right)\::\:{y}\:=\:−\frac{\mathrm{1}}{−\frac{\mathrm{1}}{\mathrm{2}}}{x}+{b}\:=\:\mathrm{2}{x}+{b} \\ $$$$\left(\mathrm{M}\right)\::\:{y}\:=\:\mathrm{2}{x}+\mathrm{36} \\ $$

Commented by pete last updated on 23/Jan/21

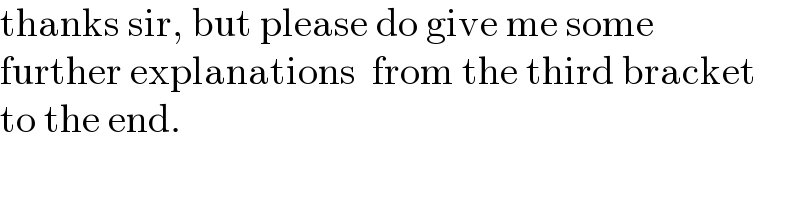
thanks sir, but please do give me some further explanations from the third bracket to the end.

$$\mathrm{thanks}\:\mathrm{sir},\:\mathrm{but}\:\mathrm{please}\:\mathrm{do}\:\mathrm{give}\:\mathrm{me}\:\mathrm{some} \\ $$$$\mathrm{further}\:\mathrm{explanations}\:\:\mathrm{from}\:\mathrm{the}\:\mathrm{third}\:\mathrm{bracket} \\ $$$$\mathrm{to}\:\mathrm{the}\:\mathrm{end}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com