
Question Number 130092 by Adel last updated on 22/Jan/21
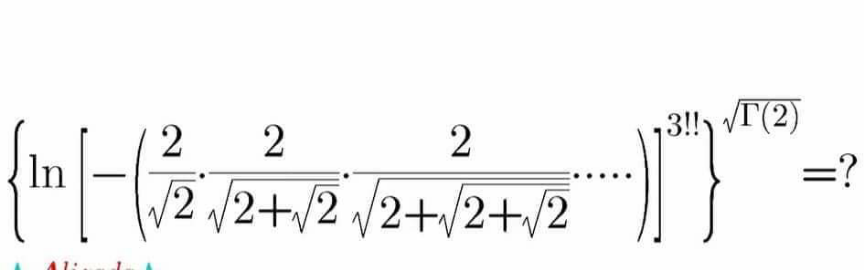
Commented by 0731619177 last updated on 24/Jan/21

$${hhhh} \\ $$
Answered by Dwaipayan Shikari last updated on 22/Jan/21
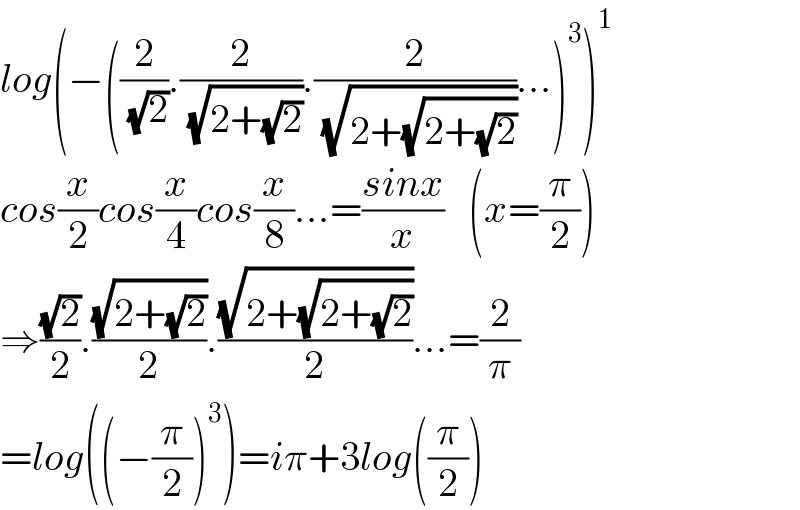
$${log}\left(−\left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{2}}}.\frac{\mathrm{2}}{\:\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}.\frac{\mathrm{2}}{\:\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}}...\right)^{\mathrm{3}} \right)^{\mathrm{1}} \\ $$$${cos}\frac{{x}}{\mathrm{2}}{cos}\frac{{x}}{\mathrm{4}}{cos}\frac{{x}}{\mathrm{8}}...=\frac{{sinx}}{{x}}\:\:\:\left({x}=\frac{\pi}{\mathrm{2}}\right) \\ $$$$\Rightarrow\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}.\frac{\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}{\mathrm{2}}.\frac{\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}}{\mathrm{2}}...=\frac{\mathrm{2}}{\pi} \\ $$$$={log}\left(\left(−\frac{\pi}{\mathrm{2}}\right)^{\mathrm{3}} \right)={i}\pi+\mathrm{3}{log}\left(\frac{\pi}{\mathrm{2}}\right) \\ $$
