
Question Number 129890 by 0731619177 last updated on 20/Jan/21
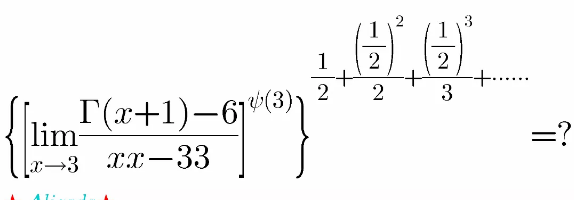
Answered by Olaf last updated on 20/Jan/21
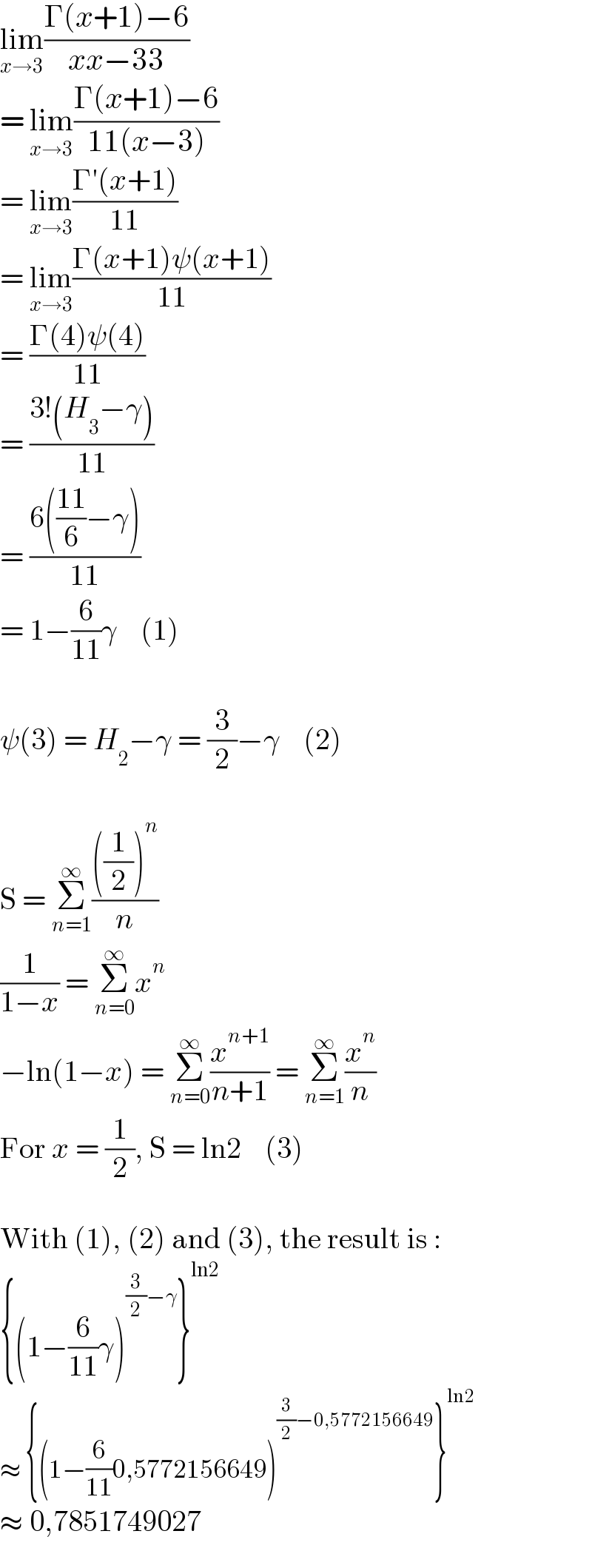
$$\underset{{x}\rightarrow\mathrm{3}} {\mathrm{lim}}\frac{\Gamma\left({x}+\mathrm{1}\right)−\mathrm{6}}{{xx}−\mathrm{33}} \\ $$$$=\:\underset{{x}\rightarrow\mathrm{3}} {\mathrm{lim}}\frac{\Gamma\left({x}+\mathrm{1}\right)−\mathrm{6}}{\mathrm{11}\left({x}−\mathrm{3}\right)} \\ $$$$=\:\underset{{x}\rightarrow\mathrm{3}} {\mathrm{lim}}\frac{\Gamma'\left({x}+\mathrm{1}\right)}{\mathrm{11}} \\ $$$$=\:\underset{{x}\rightarrow\mathrm{3}} {\mathrm{lim}}\frac{\Gamma\left({x}+\mathrm{1}\right)\psi\left({x}+\mathrm{1}\right)}{\mathrm{11}} \\ $$$$=\:\frac{\Gamma\left(\mathrm{4}\right)\psi\left(\mathrm{4}\right)}{\mathrm{11}} \\ $$$$=\:\frac{\mathrm{3}!\left({H}_{\mathrm{3}} −\gamma\right)}{\mathrm{11}} \\ $$$$=\:\frac{\mathrm{6}\left(\frac{\mathrm{11}}{\mathrm{6}}−\gamma\right)}{\mathrm{11}} \\ $$$$=\:\mathrm{1}−\frac{\mathrm{6}}{\mathrm{11}}\gamma\:\:\:\:\left(\mathrm{1}\right) \\ $$$$ \\ $$$$\psi\left(\mathrm{3}\right)\:=\:{H}_{\mathrm{2}} −\gamma\:=\:\frac{\mathrm{3}}{\mathrm{2}}−\gamma\:\:\:\:\left(\mathrm{2}\right) \\ $$$$ \\ $$$$\mathrm{S}\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} }{{n}} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}−{x}}\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{x}^{{n}} \\ $$$$−\mathrm{ln}\left(\mathrm{1}−{x}\right)\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}} \\ $$$$\mathrm{For}\:{x}\:=\:\frac{\mathrm{1}}{\mathrm{2}},\:\mathrm{S}\:=\:\mathrm{ln2}\:\:\:\:\left(\mathrm{3}\right) \\ $$$$ \\ $$$$\mathrm{With}\:\left(\mathrm{1}\right),\:\left(\mathrm{2}\right)\:\mathrm{and}\:\left(\mathrm{3}\right),\:\mathrm{the}\:\mathrm{result}\:\mathrm{is}\:: \\ $$$$\left\{\left(\mathrm{1}−\frac{\mathrm{6}}{\mathrm{11}}\gamma\right)^{\frac{\mathrm{3}}{\mathrm{2}}−\gamma} \right\}^{\mathrm{ln2}} \\ $$$$\approx\:\left\{\left(\mathrm{1}−\frac{\mathrm{6}}{\mathrm{11}}\mathrm{0},\mathrm{5772156649}\right)^{\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{0},\mathrm{5772156649}} \right\}^{\mathrm{ln2}} \\ $$$$\approx\:\mathrm{0},\mathrm{7851749027} \\ $$
