Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 129320 by ajfour last updated on 14/Jan/21

Commented by gaferrafie last updated on 14/Jan/21

سلام چطور میشه تو خروجی آدرس سایت را حذف کرد

Answered by ajfour last updated on 14/Jan/21

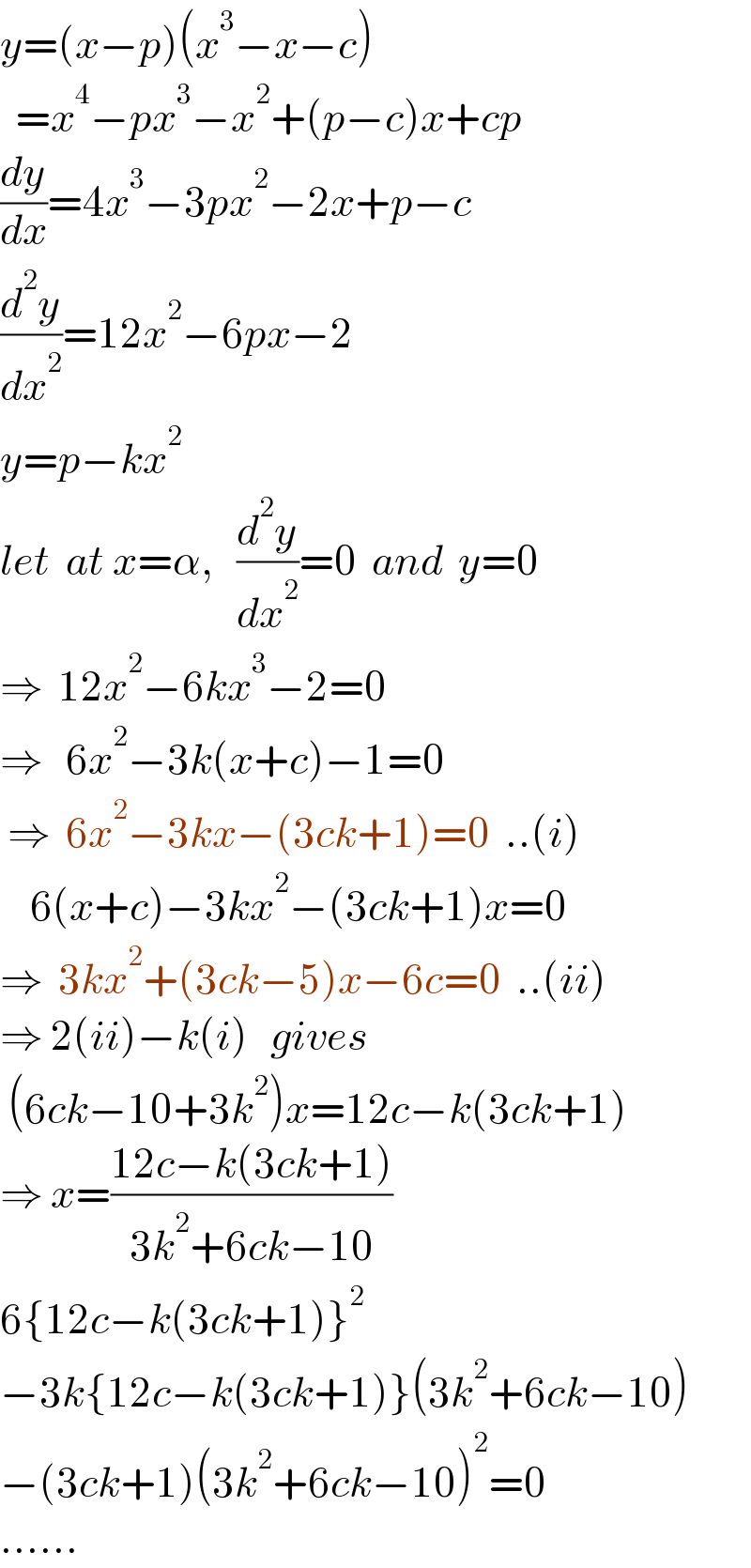
y=(x−p)(x^3 −x−c) =x^4 −px^3 −x^2 +(p−c)x+cp (dy/dx)=4x^3 −3px^2 −2x+p−c (d^2 y/dx^2 )=12x^2 −6px−2 y=p−kx^2 let at x=α, (d^2 y/dx^2 )=0 and y=0 ⇒ 12x^2 −6kx^3 −2=0 ⇒ 6x^2 −3k(x+c)−1=0 ⇒ 6x^2 −3kx−(3ck+1)=0 ..(i) 6(x+c)−3kx^2 −(3ck+1)x=0 ⇒ 3kx^2 +(3ck−5)x−6c=0 ..(ii) ⇒ 2(ii)−k(i) gives (6ck−10+3k^2 )x=12c−k(3ck+1) ⇒ x=((12c−k(3ck+1))/(3k^2 +6ck−10)) 6{12c−k(3ck+1)}^2 −3k{12c−k(3ck+1)}(3k^2 +6ck−10) −(3ck+1)(3k^2 +6ck−10)^2 =0 ......

$${y}=\left({x}−{p}\right)\left({x}^{\mathrm{3}} −{x}−{c}\right) \\ $$$$\:\:={x}^{\mathrm{4}} −{px}^{\mathrm{3}} −{x}^{\mathrm{2}} +\left({p}−{c}\right){x}+{cp} \\ $$$$\frac{{dy}}{{dx}}=\mathrm{4}{x}^{\mathrm{3}} −\mathrm{3}{px}^{\mathrm{2}} −\mathrm{2}{x}+{p}−{c} \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\mathrm{12}{x}^{\mathrm{2}} −\mathrm{6}{px}−\mathrm{2} \\ $$$${y}={p}−{kx}^{\mathrm{2}} \\ $$$${let}\:\:{at}\:{x}=\alpha,\:\:\:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\mathrm{0}\:\:{and}\:\:{y}=\mathrm{0} \\ $$$$\Rightarrow\:\:\mathrm{12}{x}^{\mathrm{2}} −\mathrm{6}{kx}^{\mathrm{3}} −\mathrm{2}=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\mathrm{6}{x}^{\mathrm{2}} −\mathrm{3}{k}\left({x}+{c}\right)−\mathrm{1}=\mathrm{0} \\ $$$$\:\Rightarrow\:\:\mathrm{6}{x}^{\mathrm{2}} −\mathrm{3}{kx}−\left(\mathrm{3}{ck}+\mathrm{1}\right)=\mathrm{0}\:\:..\left({i}\right) \\ $$$$\:\:\:\:\mathrm{6}\left({x}+{c}\right)−\mathrm{3}{kx}^{\mathrm{2}} −\left(\mathrm{3}{ck}+\mathrm{1}\right){x}=\mathrm{0} \\ $$$$\Rightarrow\:\:\mathrm{3}{kx}^{\mathrm{2}} +\left(\mathrm{3}{ck}−\mathrm{5}\right){x}−\mathrm{6}{c}=\mathrm{0}\:\:..\left({ii}\right) \\ $$$$\Rightarrow\:\mathrm{2}\left({ii}\right)−{k}\left({i}\right)\:\:\:{gives} \\ $$$$\:\left(\mathrm{6}{ck}−\mathrm{10}+\mathrm{3}{k}^{\mathrm{2}} \right){x}=\mathrm{12}{c}−{k}\left(\mathrm{3}{ck}+\mathrm{1}\right) \\ $$$$\Rightarrow\:{x}=\frac{\mathrm{12}{c}−{k}\left(\mathrm{3}{ck}+\mathrm{1}\right)}{\mathrm{3}{k}^{\mathrm{2}} +\mathrm{6}{ck}−\mathrm{10}} \\ $$$$\mathrm{6}\left\{\mathrm{12}{c}−{k}\left(\mathrm{3}{ck}+\mathrm{1}\right)\right\}^{\mathrm{2}} \\ $$$$−\mathrm{3}{k}\left\{\mathrm{12}{c}−{k}\left(\mathrm{3}{ck}+\mathrm{1}\right)\right\}\left(\mathrm{3}{k}^{\mathrm{2}} +\mathrm{6}{ck}−\mathrm{10}\right) \\ $$$$−\left(\mathrm{3}{ck}+\mathrm{1}\right)\left(\mathrm{3}{k}^{\mathrm{2}} +\mathrm{6}{ck}−\mathrm{10}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$...... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com