
Question Number 129102 by AbdulAzizabir last updated on 12/Jan/21
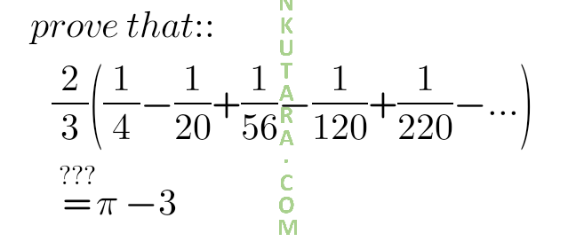
Answered by Olaf last updated on 12/Jan/21
![Σ_(k=1) ^n k^2 = {1, 5, 14, 30, 55,...} = ((n(n+1)(2n+1))/6) S = (2/3)((1/4)−(1/(20))+(1/(56))−(1/(120))+(1/(220))−...) S = (1/6)((1/1)−(1/5)+(1/(14))−(1/(30))+(1/(55))−...) S = (1/6)Σ_(n=1) ^∞ (((−1)^(n+1) )/((n(n+1)(2n+1))/6)) S = Σ_(n=1) ^∞ (((−1)^(n+1) )/(n(n+1)(2n+1))) S = Σ_(n=1) ^∞ (−1)^(n+1) [(1/n)+(1/(n+1))−(4/(2n+1))] S = −Σ_(n=1) ^∞ (((−1)^n )/n)+Σ_(n=1) ^∞ (((−1)^(n+1) )/(n+1))+4Σ_(n=1) ^∞ (((−1)^n )/(2n+1)) S = −Σ_(n=1) ^∞ (((−1)^n )/n)+Σ_(n=1) ^∞ (((−1)^n )/n)+1+4Σ_(n=1) ^∞ (((−1)^n )/(2n+1)) S = 4Σ_(n=1) ^∞ (((−1)^n )/(2n+1))+1 (1/(1+x^2 )) = Σ_(n=0) ^∞ (−1)^n x^(2n) arctanx = Σ_(n=0) ^∞ (((−1)^n )/(2n+1))x^(2n+1) arctan(1) = Σ_(n=0) ^∞ (((−1)^n )/(2n+1)) = (π/4) and Σ_(n=1) ^∞ (((−1)^n )/(2n+1)) = (π/4)−1 ⇒ S = 4((π/4)−1)+1 = π−3](Q129106.png)
$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{\mathrm{2}} \:=\:\left\{\mathrm{1},\:\mathrm{5},\:\mathrm{14},\:\mathrm{30},\:\mathrm{55},...\right\}\:=\:\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}} \\ $$$$\mathrm{S}\:=\:\frac{\mathrm{2}}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{20}}+\frac{\mathrm{1}}{\mathrm{56}}−\frac{\mathrm{1}}{\mathrm{120}}+\frac{\mathrm{1}}{\mathrm{220}}−...\right) \\ $$$$\mathrm{S}\:=\:\frac{\mathrm{1}}{\mathrm{6}}\left(\frac{\mathrm{1}}{\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{14}}−\frac{\mathrm{1}}{\mathrm{30}}+\frac{\mathrm{1}}{\mathrm{55}}−...\right) \\ $$$$\mathrm{S}\:=\:\frac{\mathrm{1}}{\mathrm{6}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}}} \\ $$$$\mathrm{S}\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)} \\ $$$$\mathrm{S}\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \left[\frac{\mathrm{1}}{{n}}+\frac{\mathrm{1}}{{n}+\mathrm{1}}−\frac{\mathrm{4}}{\mathrm{2}{n}+\mathrm{1}}\right] \\ $$$$\mathrm{S}\:=\:−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}+\mathrm{4}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{1}} \\ $$$$\mathrm{S}\:=\:−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}+\mathrm{1}+\mathrm{4}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{1}} \\ $$$$\mathrm{S}\:=\:\mathrm{4}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{1}}+\mathrm{1} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{2}{n}} \\ $$$$\mathrm{arctan}{x}\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{1}}{x}^{\mathrm{2}{n}+\mathrm{1}} \\ $$$$\mathrm{arctan}\left(\mathrm{1}\right)\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{1}}\:=\:\frac{\pi}{\mathrm{4}} \\ $$$$\mathrm{and}\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{1}}\:=\:\frac{\pi}{\mathrm{4}}−\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{S}\:=\:\mathrm{4}\left(\frac{\pi}{\mathrm{4}}−\mathrm{1}\right)+\mathrm{1}\:=\:\pi−\mathrm{3} \\ $$
