
Question Number 129088 by Gulnoza last updated on 12/Jan/21

Answered by MJS_new last updated on 12/Jan/21
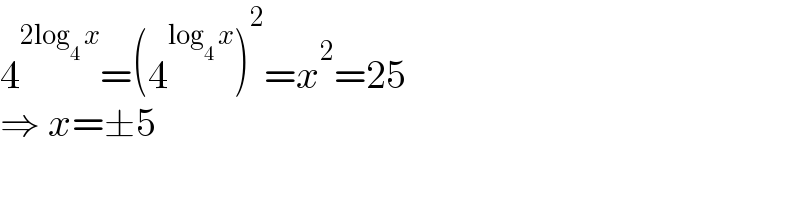
$$\mathrm{4}^{\mathrm{2log}_{\mathrm{4}} \:{x}} =\left(\mathrm{4}^{\mathrm{log}_{\mathrm{4}} \:{x}} \right)^{\mathrm{2}} ={x}^{\mathrm{2}} =\mathrm{25} \\ $$$$\Rightarrow\:{x}=\pm\mathrm{5} \\ $$
Commented by hknkrc46 last updated on 12/Jan/21
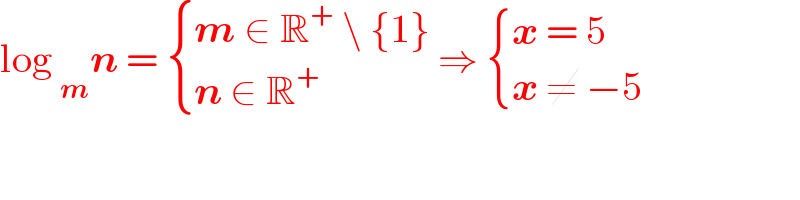
$$\mathrm{log}\:_{\boldsymbol{{m}}} \boldsymbol{{n}}\:=\:\begin{cases}{\boldsymbol{{m}}\:\in\:\mathbb{R}^{+} \:\backslash\:\left\{\mathrm{1}\right\}}\\{\boldsymbol{{n}}\:\in\:\mathbb{R}^{+} }\end{cases}\:\Rightarrow\:\begin{cases}{\boldsymbol{{x}}\:=\:\mathrm{5}}\\{\boldsymbol{{x}}\:\neq\:−\mathrm{5}}\end{cases} \\ $$
Commented by MJS_new last updated on 12/Jan/21
![x∈C ln (−5) =ln 5 +iπ 4^y =e^(yln 4) = [y=2((ln x)/(ln 4))] =e^(2ln x) = [x=−5] =e^(2ln 5 +2πi) =e^(2ln 5) e^(2πi) = [e^(2πi) =1] =e^(2ln 5) =(e^(ln 5) )^2 =5^2 =25](Q129117.png)
$${x}\in\mathbb{C} \\ $$$$\mathrm{ln}\:\left(−\mathrm{5}\right)\:=\mathrm{ln}\:\mathrm{5}\:+\mathrm{i}\pi \\ $$$$\mathrm{4}^{{y}} =\mathrm{e}^{{y}\mathrm{ln}\:\mathrm{4}} = \\ $$$$\:\:\:\:\:\left[{y}=\mathrm{2}\frac{\mathrm{ln}\:{x}}{\mathrm{ln}\:\mathrm{4}}\right] \\ $$$$=\mathrm{e}^{\mathrm{2ln}\:{x}} = \\ $$$$\:\:\:\:\:\left[{x}=−\mathrm{5}\right] \\ $$$$=\mathrm{e}^{\mathrm{2ln}\:\mathrm{5}\:+\mathrm{2}\pi\mathrm{i}} =\mathrm{e}^{\mathrm{2ln}\:\mathrm{5}} \mathrm{e}^{\mathrm{2}\pi\mathrm{i}} = \\ $$$$\:\:\:\:\:\left[\mathrm{e}^{\mathrm{2}\pi\mathrm{i}} =\mathrm{1}\right] \\ $$$$=\mathrm{e}^{\mathrm{2ln}\:\mathrm{5}} =\left(\mathrm{e}^{\mathrm{ln}\:\mathrm{5}} \right)^{\mathrm{2}} =\mathrm{5}^{\mathrm{2}} =\mathrm{25} \\ $$
