Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 128849 by I want to learn more last updated on 10/Jan/21

Commented by Tawa11 last updated on 15/Sep/21

nice

$$\mathrm{nice} \\ $$

Answered by mr W last updated on 10/Jan/21

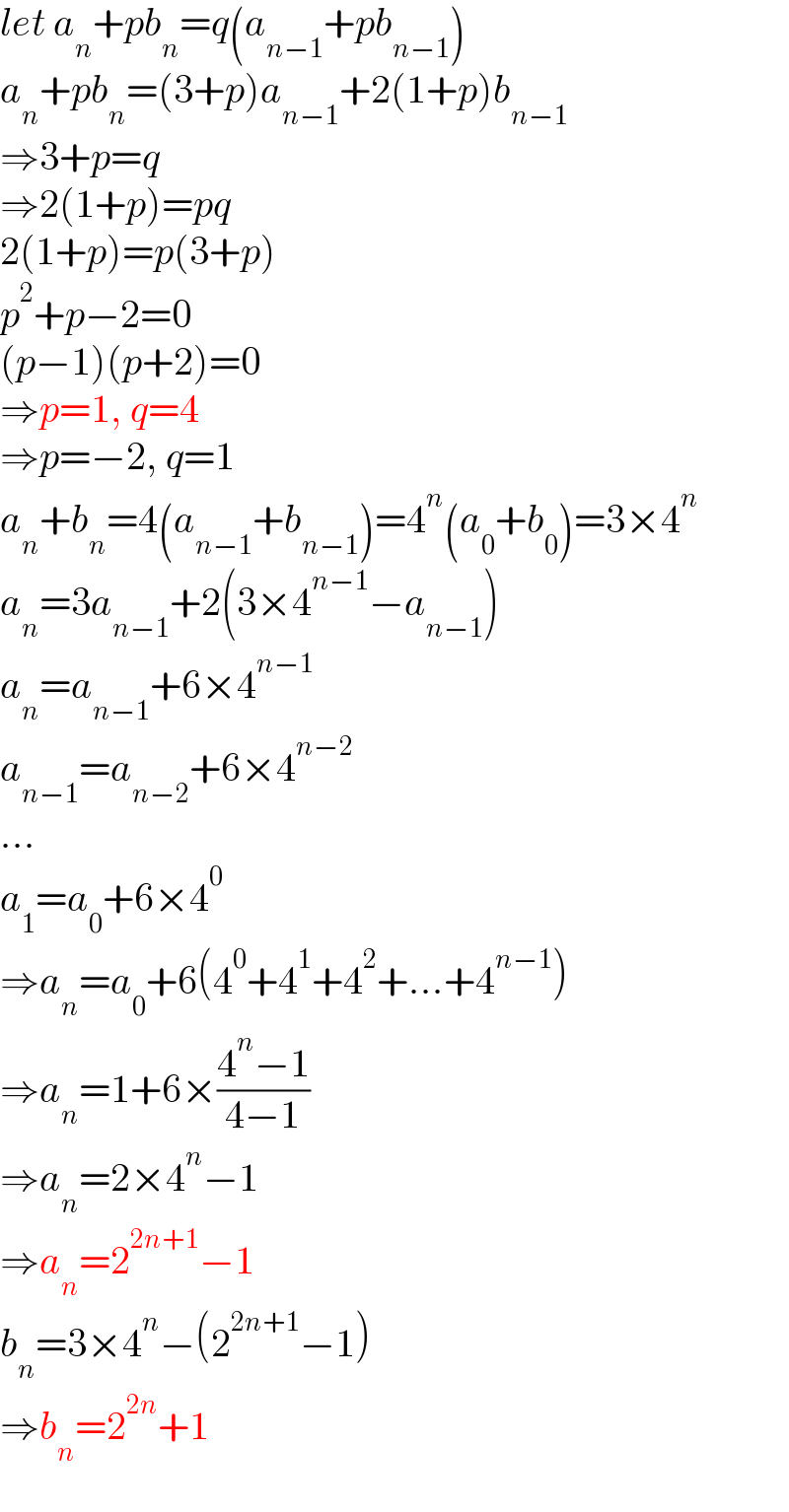
let a_n +pb_n =q(a_(n−1) +pb_(n−1) ) a_n +pb_n =(3+p)a_(n−1) +2(1+p)b_(n−1) ⇒3+p=q ⇒2(1+p)=pq 2(1+p)=p(3+p) p^2 +p−2=0 (p−1)(p+2)=0 ⇒p=1, q=4 ⇒p=−2, q=1 a_n +b_n =4(a_(n−1) +b_(n−1) )=4^n (a_0 +b_0 )=3×4^n a_n =3a_(n−1) +2(3×4^(n−1) −a_(n−1) ) a_n =a_(n−1) +6×4^(n−1) a_(n−1) =a_(n−2) +6×4^(n−2) ... a_1 =a_0 +6×4^0 ⇒a_n =a_0 +6(4^0 +4^1 +4^2 +...+4^(n−1) ) ⇒a_n =1+6×((4^n −1)/(4−1)) ⇒a_n =2×4^n −1 ⇒a_n =2^(2n+1) −1 b_n =3×4^n −(2^(2n+1) −1) ⇒b_n =2^(2n) +1

$${let}\:{a}_{{n}} +{pb}_{{n}} ={q}\left({a}_{{n}−\mathrm{1}} +{pb}_{{n}−\mathrm{1}} \right) \\ $$$${a}_{{n}} +{pb}_{{n}} =\left(\mathrm{3}+{p}\right){a}_{{n}−\mathrm{1}} +\mathrm{2}\left(\mathrm{1}+{p}\right){b}_{{n}−\mathrm{1}} \\ $$$$\Rightarrow\mathrm{3}+{p}={q} \\ $$$$\Rightarrow\mathrm{2}\left(\mathrm{1}+{p}\right)={pq} \\ $$$$\mathrm{2}\left(\mathrm{1}+{p}\right)={p}\left(\mathrm{3}+{p}\right) \\ $$$${p}^{\mathrm{2}} +{p}−\mathrm{2}=\mathrm{0} \\ $$$$\left({p}−\mathrm{1}\right)\left({p}+\mathrm{2}\right)=\mathrm{0} \\ $$$$\Rightarrow{p}=\mathrm{1},\:{q}=\mathrm{4} \\ $$$$\Rightarrow{p}=−\mathrm{2},\:{q}=\mathrm{1} \\ $$$${a}_{{n}} +{b}_{{n}} =\mathrm{4}\left({a}_{{n}−\mathrm{1}} +{b}_{{n}−\mathrm{1}} \right)=\mathrm{4}^{{n}} \left({a}_{\mathrm{0}} +{b}_{\mathrm{0}} \right)=\mathrm{3}×\mathrm{4}^{{n}} \\ $$$${a}_{{n}} =\mathrm{3}{a}_{{n}−\mathrm{1}} +\mathrm{2}\left(\mathrm{3}×\mathrm{4}^{{n}−\mathrm{1}} −{a}_{{n}−\mathrm{1}} \right) \\ $$$${a}_{{n}} ={a}_{{n}−\mathrm{1}} +\mathrm{6}×\mathrm{4}^{{n}−\mathrm{1}} \\ $$$${a}_{{n}−\mathrm{1}} ={a}_{{n}−\mathrm{2}} +\mathrm{6}×\mathrm{4}^{{n}−\mathrm{2}} \\ $$$$... \\ $$$${a}_{\mathrm{1}} ={a}_{\mathrm{0}} +\mathrm{6}×\mathrm{4}^{\mathrm{0}} \\ $$$$\Rightarrow{a}_{{n}} ={a}_{\mathrm{0}} +\mathrm{6}\left(\mathrm{4}^{\mathrm{0}} +\mathrm{4}^{\mathrm{1}} +\mathrm{4}^{\mathrm{2}} +...+\mathrm{4}^{{n}−\mathrm{1}} \right) \\ $$$$\Rightarrow{a}_{{n}} =\mathrm{1}+\mathrm{6}×\frac{\mathrm{4}^{{n}} −\mathrm{1}}{\mathrm{4}−\mathrm{1}} \\ $$$$\Rightarrow{a}_{{n}} =\mathrm{2}×\mathrm{4}^{{n}} −\mathrm{1} \\ $$$$\Rightarrow{a}_{{n}} =\mathrm{2}^{\mathrm{2}{n}+\mathrm{1}} −\mathrm{1} \\ $$$${b}_{{n}} =\mathrm{3}×\mathrm{4}^{{n}} −\left(\mathrm{2}^{\mathrm{2}{n}+\mathrm{1}} −\mathrm{1}\right) \\ $$$$\Rightarrow{b}_{{n}} =\mathrm{2}^{\mathrm{2}{n}} +\mathrm{1} \\ $$

Commented by I want to learn more last updated on 10/Jan/21

Thanks sir, i appreciate.

$$\mathrm{Thanks}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{appreciate}. \\ $$

Answered by mathmax by abdo last updated on 11/Jan/21

{ ((a_n =3a_(n−1) +2b_(n−1) ((a_n ),(b_n ) ))),((b_n =a_(n−1) +2b_(n−1) ⇒)) :}= (((3 2)),((1 2)) ) ((a_(n−1) ),(b_(n−1) ) ) ⇒ ((a_n ),(b_n ) ) =M^n ((a_0 ),(b_0 ) ) with M = (((3 2)),((1 2)) ) the problem lead to find M^n p_c (x)=det(M−xI)= determinant (((3−x 2)),((1 2−x)))=(3−x)(2−x)−2 =6−3x−2x+x^2 −2 =x^2 −5x+4 =x^2 −1 −5x+5 =(x−1)(x+1)−5(x−1) =(x−1)(x−4) so propre values are λ_1 =1 and λ_2 =4 let divide x^(n ) by P_c (M) ⇒ x^n =P_c (x)q(x)+u_n x +v_n ⇒1^n =u_n +v_n and4^n =4u_n +v_n ⇒ { ((u_n +v_n =1 { ((u_n =((4^n −1)/3))),((v_n =1−((4^n −1)/3))) :})),((4u_n +v_n =4^(n ) ⇒)) :} ⇒ { ((u_n =((4^n −1)/3) ⇒ { ((u_n =((4^n −1)/3))),((v_n =((4−4^n )/3))) :})),((v_n =((3−4^n +1)/3))) :} M^n =u_n M+v_n I_2 (cayley P_c (M)=0) ⇒M^n =((4^n −1)/3) (((3 2)),((1 2)) ) +((4−4^n )/3) (((1 0)),((0 1)) ) = (((4^n −1 (2/3)(4^n −1))),((((4^n −1)/3) (2/3)(4^n −1))) ) + (((((4−4^n )/3) 0)),((0 ((4−4^n )/3))) ) = (((((3.4^n −3+4−4^n )/3) (2/3)(4^n −1))),((((4^n −1)/3) ((2.4^n −2+4−4^n )/3))) ) = (((((2.4^n +1)/3) (2/3)(4^n −1))),((((4^n −1)/3) ((4^n +2)/3))) ) ⇒ ((a_n ),(b_n ) )=(1/3) (((2.4^n +1 2.4^n −2)),((4^n −1 4^n +2)) ) . ((1),(2) ) =(1/3) (((2.4^n +1+4.4^n −4)),((4^n −1 +2.4^n +4)) )=(1/3) (((6.4^n −3)),((3.4^n +3)) ) = (((2.4^n −1)),((4^n +1)) ) ⇒ a_n =2.4^n −1 and v_n =4^n +1

$$\begin{cases}{\mathrm{a}_{\mathrm{n}} =\mathrm{3a}_{\mathrm{n}−\mathrm{1}} +\mathrm{2b}_{\mathrm{n}−\mathrm{1}} \:\:\:\:\:\:\:\:\:\:\:\begin{pmatrix}{\mathrm{a}_{\mathrm{n}} }\\{\mathrm{b}_{\mathrm{n}} }\end{pmatrix}}\\{\mathrm{b}_{\mathrm{n}} =\mathrm{a}_{\mathrm{n}−\mathrm{1}} +\mathrm{2b}_{\mathrm{n}−\mathrm{1}} \:\:\:\:\:\Rightarrow}\end{cases}=\begin{pmatrix}{\mathrm{3}\:\:\:\:\:\:\:\:\mathrm{2}}\\{\mathrm{1}\:\:\:\:\:\:\:\:\:\mathrm{2}}\end{pmatrix}\begin{pmatrix}{\mathrm{a}_{\mathrm{n}−\mathrm{1}} }\\{\mathrm{b}_{\mathrm{n}−\mathrm{1}} }\end{pmatrix} \\ $$$$\Rightarrow\begin{pmatrix}{\mathrm{a}_{\mathrm{n}} }\\{\mathrm{b}_{\mathrm{n}} }\end{pmatrix}\:=\mathrm{M}^{\mathrm{n}} \begin{pmatrix}{\mathrm{a}_{\mathrm{0}} }\\{\mathrm{b}_{\mathrm{0}} }\end{pmatrix}\:\mathrm{with}\:\mathrm{M}\:=\begin{pmatrix}{\mathrm{3}\:\:\:\:\:\:\:\:\:\:\mathrm{2}}\\{\mathrm{1}\:\:\:\:\:\:\:\:\:\:\mathrm{2}}\end{pmatrix}\:\:\mathrm{the}\:\mathrm{problem}\:\mathrm{lead}\:\mathrm{to}\:\mathrm{find}\:\mathrm{M}^{\mathrm{n}} \\ $$$$\mathrm{p}_{\mathrm{c}} \left(\mathrm{x}\right)=\mathrm{det}\left(\mathrm{M}−\mathrm{xI}\right)=\begin{vmatrix}{\mathrm{3}−\mathrm{x}\:\:\:\:\:\:\:\:\:\:\mathrm{2}}\\{\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}−\mathrm{x}}\end{vmatrix}=\left(\mathrm{3}−\mathrm{x}\right)\left(\mathrm{2}−\mathrm{x}\right)−\mathrm{2} \\ $$$$=\mathrm{6}−\mathrm{3x}−\mathrm{2x}+\mathrm{x}^{\mathrm{2}} −\mathrm{2}\:=\mathrm{x}^{\mathrm{2}} −\mathrm{5x}+\mathrm{4}\:=\mathrm{x}^{\mathrm{2}} −\mathrm{1}\:−\mathrm{5x}+\mathrm{5} \\ $$$$=\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}+\mathrm{1}\right)−\mathrm{5}\left(\mathrm{x}−\mathrm{1}\right)\:=\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}−\mathrm{4}\right)\:\mathrm{so}\:\mathrm{propre}\:\mathrm{values}\:\mathrm{are} \\ $$$$\lambda_{\mathrm{1}} =\mathrm{1}\:\mathrm{and}\:\lambda_{\mathrm{2}} =\mathrm{4}\:\:\:\:\mathrm{let}\:\mathrm{divide}\:\mathrm{x}^{\mathrm{n}\:} \:\mathrm{by}\:\mathrm{P}_{\mathrm{c}} \left(\mathrm{M}\right)\:\Rightarrow \\ $$$$\mathrm{x}^{\mathrm{n}} \:=\mathrm{P}_{\mathrm{c}} \left(\mathrm{x}\right)\mathrm{q}\left(\mathrm{x}\right)+\mathrm{u}_{\mathrm{n}} \mathrm{x}\:+\mathrm{v}_{\mathrm{n}} \:\Rightarrow\mathrm{1}^{\mathrm{n}} \:=\mathrm{u}_{\mathrm{n}} \:+\mathrm{v}_{\mathrm{n}} \:\mathrm{and4}^{\mathrm{n}} \:=\mathrm{4u}_{\mathrm{n}} \:+\mathrm{v}_{\mathrm{n}} \:\Rightarrow\: \\ $$$$\begin{cases}{\mathrm{u}_{\mathrm{n}} \:+\mathrm{v}_{\mathrm{n}} =\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\begin{cases}{\mathrm{u}_{\mathrm{n}} =\frac{\mathrm{4}^{\mathrm{n}} −\mathrm{1}}{\mathrm{3}}}\\{\mathrm{v}_{\mathrm{n}} =\mathrm{1}−\frac{\mathrm{4}^{\mathrm{n}} −\mathrm{1}}{\mathrm{3}}}\end{cases}}\\{\mathrm{4u}_{\mathrm{n}} \:+\mathrm{v}_{\mathrm{n}} =\mathrm{4}^{\mathrm{n}\:\:} \:\:\:\:\Rightarrow}\end{cases} \\ $$$$\Rightarrow\begin{cases}{\mathrm{u}_{\mathrm{n}} =\frac{\mathrm{4}^{\mathrm{n}} −\mathrm{1}}{\mathrm{3}}\:\:\:\:\Rightarrow\:\:\begin{cases}{\mathrm{u}_{\mathrm{n}} =\frac{\mathrm{4}^{\mathrm{n}} −\mathrm{1}}{\mathrm{3}}}\\{\mathrm{v}_{\mathrm{n}} =\frac{\mathrm{4}−\mathrm{4}^{\mathrm{n}} }{\mathrm{3}}}\end{cases}}\\{\mathrm{v}_{\mathrm{n}} =\frac{\mathrm{3}−\mathrm{4}^{\mathrm{n}} +\mathrm{1}}{\mathrm{3}}}\end{cases} \\ $$$$\mathrm{M}^{\mathrm{n}} \:=\mathrm{u}_{\mathrm{n}} \mathrm{M}+\mathrm{v}_{\mathrm{n}} \:\mathrm{I}_{\mathrm{2}} \:\:\:\:\left(\mathrm{cayley}\:\:\mathrm{P}_{\mathrm{c}} \left(\mathrm{M}\right)=\mathrm{0}\right) \\ $$$$\Rightarrow\mathrm{M}^{\mathrm{n}} \:=\frac{\mathrm{4}^{\mathrm{n}} −\mathrm{1}}{\mathrm{3}}\begin{pmatrix}{\mathrm{3}\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}}\\{\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}}\end{pmatrix}\:+\frac{\mathrm{4}−\mathrm{4}^{\mathrm{n}} }{\mathrm{3}}\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{0}\:\:\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix} \\ $$$$=\begin{pmatrix}{\mathrm{4}^{\mathrm{n}} −\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{4}^{\mathrm{n}} −\mathrm{1}\right)}\\{\frac{\mathrm{4}^{\mathrm{n}} −\mathrm{1}}{\mathrm{3}}\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{4}^{\mathrm{n}} −\mathrm{1}\right)}\end{pmatrix}\:\:+\begin{pmatrix}{\frac{\mathrm{4}−\mathrm{4}^{\mathrm{n}} }{\mathrm{3}}\:\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{4}−\mathrm{4}^{\mathrm{n}} }{\mathrm{3}}}\end{pmatrix} \\ $$$$=\begin{pmatrix}{\frac{\mathrm{3}.\mathrm{4}^{\mathrm{n}} −\mathrm{3}+\mathrm{4}−\mathrm{4}^{\mathrm{n}} }{\mathrm{3}}\:\:\:\:\:\:\:\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{4}^{\mathrm{n}} −\mathrm{1}\right)}\\{\frac{\mathrm{4}^{\mathrm{n}} −\mathrm{1}}{\mathrm{3}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{2}.\mathrm{4}^{\mathrm{n}} −\mathrm{2}+\mathrm{4}−\mathrm{4}^{\mathrm{n}} }{\mathrm{3}}}\end{pmatrix} \\ $$$$=\begin{pmatrix}{\frac{\mathrm{2}.\mathrm{4}^{\mathrm{n}} +\mathrm{1}}{\mathrm{3}}\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{4}^{\mathrm{n}} −\mathrm{1}\right)}\\{\frac{\mathrm{4}^{\mathrm{n}} −\mathrm{1}}{\mathrm{3}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{4}^{\mathrm{n}} +\mathrm{2}}{\mathrm{3}}}\end{pmatrix} \\ $$$$\Rightarrow\begin{pmatrix}{\mathrm{a}_{\mathrm{n}} }\\{\mathrm{b}_{\mathrm{n}} }\end{pmatrix}=\frac{\mathrm{1}}{\mathrm{3}}\begin{pmatrix}{\mathrm{2}.\mathrm{4}^{\mathrm{n}} +\mathrm{1}\:\:\:\:\:\:\:\mathrm{2}.\mathrm{4}^{\mathrm{n}} −\mathrm{2}}\\{\mathrm{4}^{\mathrm{n}} −\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{4}^{\mathrm{n}} \:+\mathrm{2}}\end{pmatrix}\:.\begin{pmatrix}{\mathrm{1}}\\{\mathrm{2}}\end{pmatrix} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\begin{pmatrix}{\mathrm{2}.\mathrm{4}^{\mathrm{n}} \:+\mathrm{1}+\mathrm{4}.\mathrm{4}^{\mathrm{n}} −\mathrm{4}}\\{\mathrm{4}^{\mathrm{n}} −\mathrm{1}\:+\mathrm{2}.\mathrm{4}^{\mathrm{n}} \:+\mathrm{4}}\end{pmatrix}=\frac{\mathrm{1}}{\mathrm{3}}\begin{pmatrix}{\mathrm{6}.\mathrm{4}^{\mathrm{n}} −\mathrm{3}}\\{\mathrm{3}.\mathrm{4}^{\mathrm{n}} \:+\mathrm{3}}\end{pmatrix} \\ $$$$=\begin{pmatrix}{\mathrm{2}.\mathrm{4}^{\mathrm{n}} −\mathrm{1}}\\{\mathrm{4}^{\mathrm{n}} \:+\mathrm{1}}\end{pmatrix}\:\Rightarrow\:\mathrm{a}_{\mathrm{n}} =\mathrm{2}.\mathrm{4}^{\mathrm{n}} −\mathrm{1}\:\mathrm{and}\:\mathrm{v}_{\mathrm{n}} =\mathrm{4}^{\mathrm{n}} \:+\mathrm{1} \\ $$$$ \\ $$

Commented by I want to learn more last updated on 11/Jan/21

Thanks sir, I appreciate.

$$\mathrm{Thanks}\:\mathrm{sir},\:\mathrm{I}\:\mathrm{appreciate}. \\ $$

Commented by I want to learn more last updated on 11/Jan/21

Thanks sir, i appreciate

$$\mathrm{Thanks}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{appreciate} \\ $$

Answered by Olaf last updated on 11/Jan/21

X_0 = ((1),(2) ), A = [(3,2),(1,2) ], X_n = AX_(n−1) X_n = A^n X_0 = ((a_n ),(b_n ) ) We solve det(A−λI) = 0 ⇒ (3−λ)(2−λ)−2 = 0 eigenvalues : λ_1 = 1 and λ_2 = 4 B = [(λ_1 ,0),(0,λ_2 ) ]= [(1,0),(0,4) ] A ((x),(y) ) = λ_1 ((x),(y) ) ⇒x_1 = −1 and y_1 = 1 A ((x),(y) ) = λ_2 ((x),(y) ) ⇒x_2 = 2 and y_2 = 1 eigenvectors : V_1 = (((−1)),(1) ) and V_2 = ((2),(1) ) P = [((−1),2),(1,1) ] P^(−1) = [((−(1/3)),(2/3)),((1/3),(1/3)) ] B = P^(−1) AP and A^n = PB^n P^(−1) A^n = [((−1),2),(1,1) ] [(1,0),(0,4^n ) ] [((−(1/3)),(2/3)),((1/3),(1/3)) ] A^n = [((−1),2),(1,1) ] [((−(1/3)),(2/3)),((4^n /3),(4^n /3)) ] A^n = [(((2.4^n +1)/3),((2.4^n −2)/3)),(((4^n −1)/3),((4^n +2)/3)) ] A^n = [(((2^(2n+1) +1)/3),((2^(2n+1) −2)/3)),(((2^(2n) −1)/3),((2^(2n) +2)/3)) ] X_n = A^n X_0 = (((((2^(2n+1) +1)/3)+2((2^(2n+1) −2)/3))),((((2^(2n) −1)/3)+2((2^(2n) +2)/3))) ) X_n = A^n X_0 = (((2^(2n+1) −1)),((2^(2n) +1)) )

$$\mathrm{X}_{\mathrm{0}} \:=\:\begin{pmatrix}{\mathrm{1}}\\{\mathrm{2}}\end{pmatrix},\:\mathrm{A}\:=\:\begin{bmatrix}{\mathrm{3}}&{\mathrm{2}}\\{\mathrm{1}}&{\mathrm{2}}\end{bmatrix},\:\mathrm{X}_{{n}} \:=\:\mathrm{AX}_{{n}−\mathrm{1}} \\ $$$$\mathrm{X}_{{n}} \:=\:\mathrm{A}^{{n}} \mathrm{X}_{\mathrm{0}} \:=\:\begin{pmatrix}{{a}_{{n}} }\\{{b}_{{n}} }\end{pmatrix} \\ $$$$\mathrm{We}\:\mathrm{solve}\:\mathrm{det}\left(\mathrm{A}−\lambda\mathrm{I}\right)\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\left(\mathrm{3}−\lambda\right)\left(\mathrm{2}−\lambda\right)−\mathrm{2}\:=\:\mathrm{0} \\ $$$$\mathrm{eigenvalues}\:: \\ $$$$\lambda_{\mathrm{1}} \:=\:\mathrm{1}\:\mathrm{and}\:\lambda_{\mathrm{2}} \:=\:\mathrm{4} \\ $$$$\mathrm{B}\:=\:\begin{bmatrix}{\lambda_{\mathrm{1}} }&{\mathrm{0}}\\{\mathrm{0}}&{\lambda_{\mathrm{2}} }\end{bmatrix}=\:\begin{bmatrix}{\mathrm{1}}&{\mathrm{0}}\\{\mathrm{0}}&{\mathrm{4}}\end{bmatrix} \\ $$$$\mathrm{A}\begin{pmatrix}{{x}}\\{{y}}\end{pmatrix}\:=\:\lambda_{\mathrm{1}} \begin{pmatrix}{{x}}\\{{y}}\end{pmatrix}\:\Rightarrow{x}_{\mathrm{1}} \:=\:−\mathrm{1}\:\mathrm{and}\:{y}_{\mathrm{1}} \:=\:\mathrm{1} \\ $$$$\mathrm{A}\begin{pmatrix}{{x}}\\{{y}}\end{pmatrix}\:=\:\lambda_{\mathrm{2}} \begin{pmatrix}{{x}}\\{{y}}\end{pmatrix}\:\Rightarrow{x}_{\mathrm{2}} \:=\:\mathrm{2}\:\mathrm{and}\:{y}_{\mathrm{2}} \:=\:\mathrm{1} \\ $$$$\mathrm{eigenvectors}\:: \\ $$$$\mathrm{V}_{\mathrm{1}} \:=\:\begin{pmatrix}{−\mathrm{1}}\\{\mathrm{1}}\end{pmatrix}\:\mathrm{and}\:\mathrm{V}_{\mathrm{2}} \:=\:\begin{pmatrix}{\mathrm{2}}\\{\mathrm{1}}\end{pmatrix} \\ $$$$\mathrm{P}\:=\:\begin{bmatrix}{−\mathrm{1}}&{\mathrm{2}}\\{\mathrm{1}}&{\mathrm{1}}\end{bmatrix} \\ $$$$\mathrm{P}^{−\mathrm{1}} \:=\:\begin{bmatrix}{−\frac{\mathrm{1}}{\mathrm{3}}}&{\frac{\mathrm{2}}{\mathrm{3}}}\\{\frac{\mathrm{1}}{\mathrm{3}}}&{\frac{\mathrm{1}}{\mathrm{3}}}\end{bmatrix} \\ $$$$\mathrm{B}\:=\:\mathrm{P}^{−\mathrm{1}} \mathrm{AP}\:\mathrm{and}\:\mathrm{A}^{{n}} \:=\:\mathrm{PB}^{{n}} \mathrm{P}^{−\mathrm{1}} \\ $$$$\mathrm{A}^{{n}} \:=\:\begin{bmatrix}{−\mathrm{1}}&{\mathrm{2}}\\{\mathrm{1}}&{\mathrm{1}}\end{bmatrix}\begin{bmatrix}{\mathrm{1}}&{\mathrm{0}}\\{\mathrm{0}}&{\mathrm{4}^{{n}} }\end{bmatrix}\begin{bmatrix}{−\frac{\mathrm{1}}{\mathrm{3}}}&{\frac{\mathrm{2}}{\mathrm{3}}}\\{\frac{\mathrm{1}}{\mathrm{3}}}&{\frac{\mathrm{1}}{\mathrm{3}}}\end{bmatrix} \\ $$$$\mathrm{A}^{{n}} \:=\:\begin{bmatrix}{−\mathrm{1}}&{\mathrm{2}}\\{\mathrm{1}}&{\mathrm{1}}\end{bmatrix}\begin{bmatrix}{−\frac{\mathrm{1}}{\mathrm{3}}}&{\frac{\mathrm{2}}{\mathrm{3}}}\\{\frac{\mathrm{4}^{{n}} }{\mathrm{3}}}&{\frac{\mathrm{4}^{{n}} }{\mathrm{3}}}\end{bmatrix} \\ $$$$\mathrm{A}^{{n}} \:=\:\begin{bmatrix}{\frac{\mathrm{2}.\mathrm{4}^{{n}} +\mathrm{1}}{\mathrm{3}}}&{\frac{\mathrm{2}.\mathrm{4}^{{n}} −\mathrm{2}}{\mathrm{3}}}\\{\frac{\mathrm{4}^{{n}} −\mathrm{1}}{\mathrm{3}}}&{\frac{\mathrm{4}^{{n}} +\mathrm{2}}{\mathrm{3}}}\end{bmatrix} \\ $$$$\mathrm{A}^{{n}} \:=\:\begin{bmatrix}{\frac{\mathrm{2}^{\mathrm{2}{n}+\mathrm{1}} +\mathrm{1}}{\mathrm{3}}}&{\frac{\mathrm{2}^{\mathrm{2}{n}+\mathrm{1}} −\mathrm{2}}{\mathrm{3}}}\\{\frac{\mathrm{2}^{\mathrm{2}{n}} −\mathrm{1}}{\mathrm{3}}}&{\frac{\mathrm{2}^{\mathrm{2}{n}} +\mathrm{2}}{\mathrm{3}}}\end{bmatrix} \\ $$$$\mathrm{X}_{{n}} \:=\:\mathrm{A}^{{n}} \mathrm{X}_{\mathrm{0}} \:=\:\begin{pmatrix}{\frac{\mathrm{2}^{\mathrm{2}{n}+\mathrm{1}} +\mathrm{1}}{\mathrm{3}}+\mathrm{2}\frac{\mathrm{2}^{\mathrm{2}{n}+\mathrm{1}} −\mathrm{2}}{\mathrm{3}}}\\{\frac{\mathrm{2}^{\mathrm{2}{n}} −\mathrm{1}}{\mathrm{3}}+\mathrm{2}\frac{\mathrm{2}^{\mathrm{2}{n}} +\mathrm{2}}{\mathrm{3}}}\end{pmatrix} \\ $$$$\mathrm{X}_{{n}} \:=\:\mathrm{A}^{{n}} \mathrm{X}_{\mathrm{0}} \:=\:\begin{pmatrix}{\mathrm{2}^{\mathrm{2}{n}+\mathrm{1}} −\mathrm{1}}\\{\mathrm{2}^{\mathrm{2}{n}} +\mathrm{1}}\end{pmatrix} \\ $$

Commented by I want to learn more last updated on 11/Jan/21

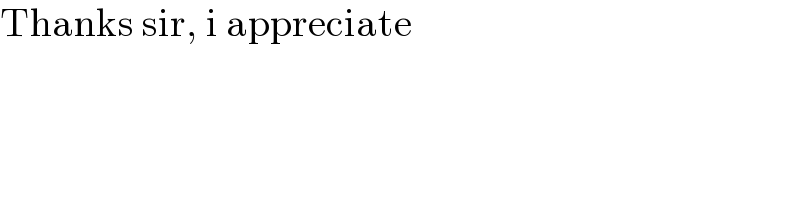
Thanks sir, i appreciate

$$\mathrm{Thanks}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{appreciate} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com