
Question Number 128652 by ajfour last updated on 09/Jan/21
Commented by ajfour last updated on 09/Jan/21

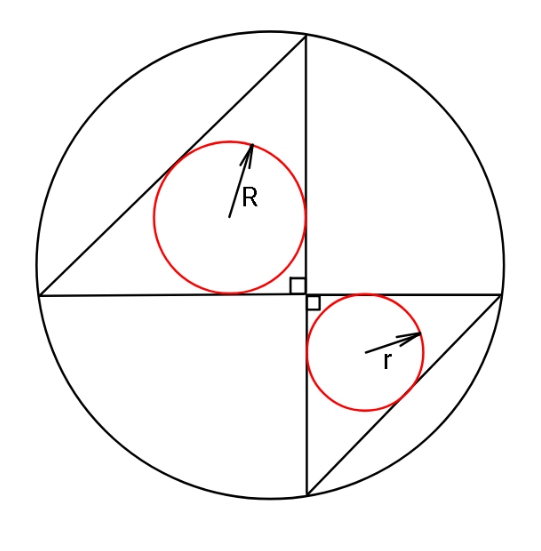
$${Find}\:{the}\:{radius}\:{of}\:{outer}\:{circle} \\ $$$${in}\:{terms}\:{of}\:{inradii}\:{R}\:{and}\:{r}\:{of} \\ $$$${two}\:{isosceles}\:{right}\:{angled}\: \\ $$$${triangles}\:\left({as}\:{shown},\:{see}\:{fig}\right). \\ $$
Answered by mr W last updated on 09/Jan/21
Commented by mr W last updated on 09/Jan/21
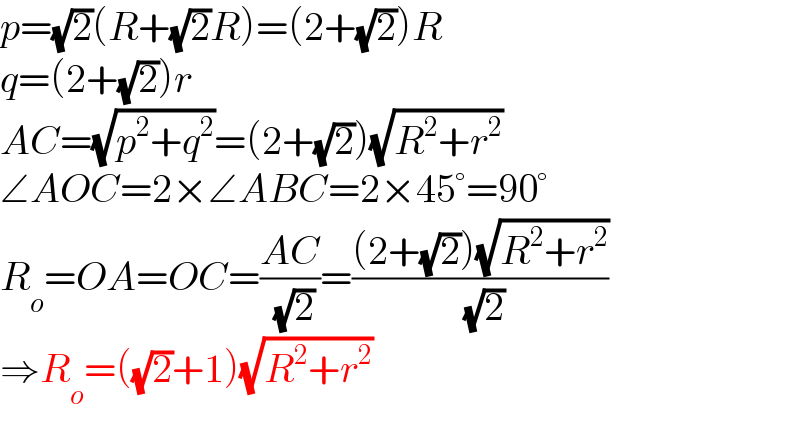
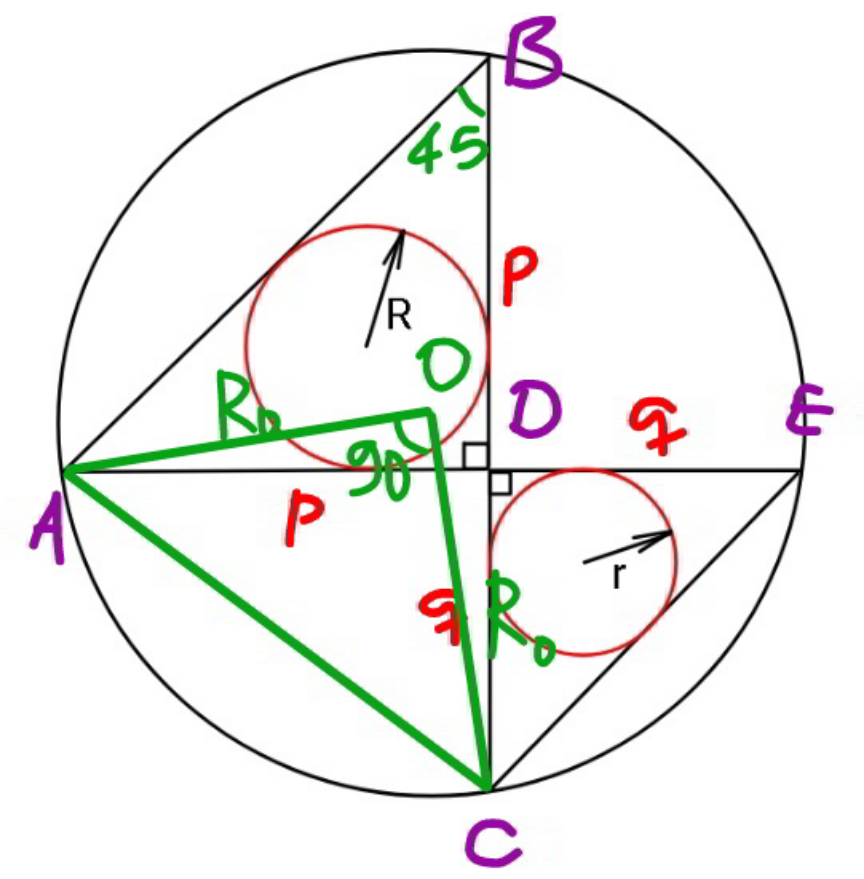
$${p}=\sqrt{\mathrm{2}}\left({R}+\sqrt{\mathrm{2}}{R}\right)=\left(\mathrm{2}+\sqrt{\mathrm{2}}\right){R} \\ $$$${q}=\left(\mathrm{2}+\sqrt{\mathrm{2}}\right){r} \\ $$$${AC}=\sqrt{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} }=\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)\sqrt{{R}^{\mathrm{2}} +{r}^{\mathrm{2}} } \\ $$$$\angle{AOC}=\mathrm{2}×\angle{ABC}=\mathrm{2}×\mathrm{45}°=\mathrm{90}° \\ $$$${R}_{{o}} ={OA}={OC}=\frac{{AC}}{\:\sqrt{\mathrm{2}}}=\frac{\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)\sqrt{{R}^{\mathrm{2}} +{r}^{\mathrm{2}} }}{\:\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow{R}_{{o}} =\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)\sqrt{{R}^{\mathrm{2}} +{r}^{\mathrm{2}} } \\ $$
Commented by ajfour last updated on 09/Jan/21
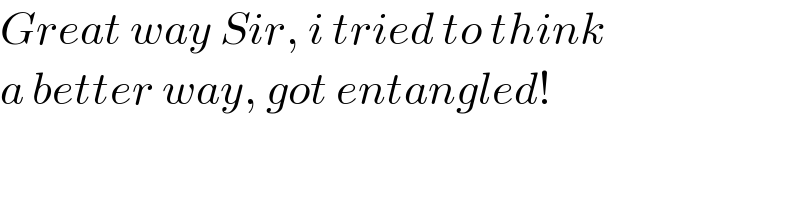
$${Great}\:{way}\:{Sir},\:{i}\:{tried}\:{to}\:{think} \\ $$$${a}\:{better}\:{way},\:{got}\:{entangled}! \\ $$
