
Question Number 128457 by SLVR last updated on 07/Jan/21
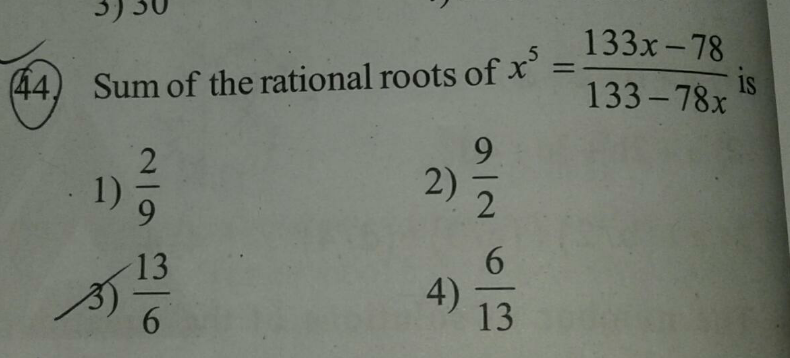
Commented by BHOOPENDRA last updated on 07/Jan/21
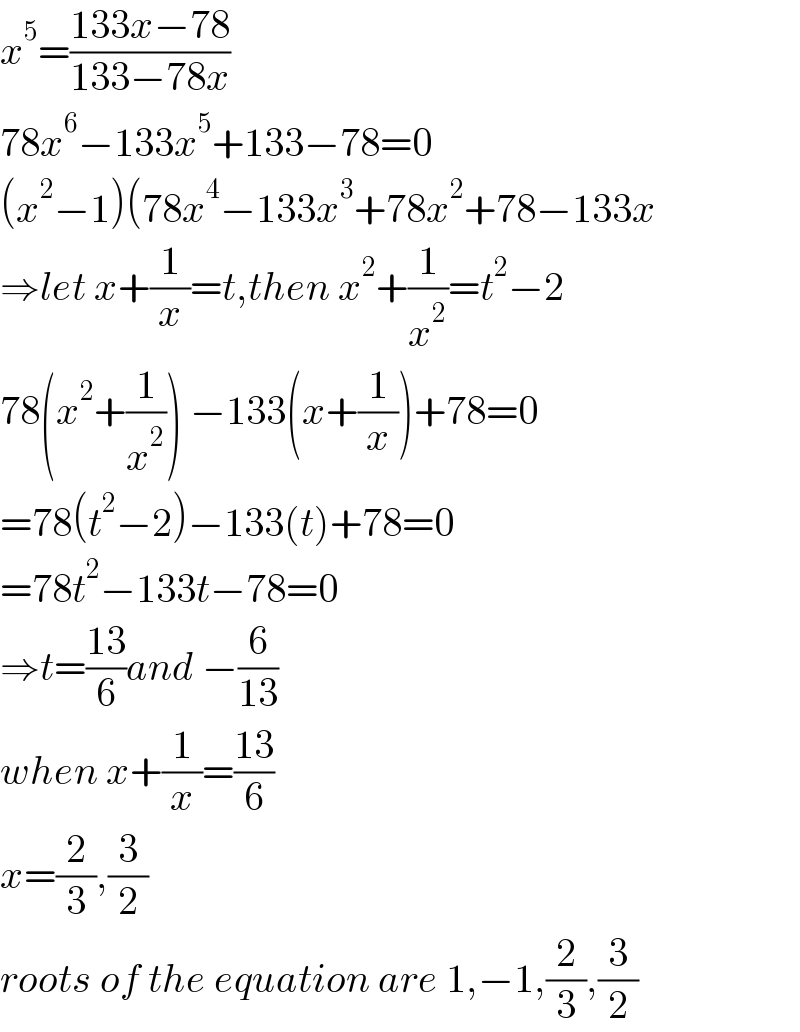
$${x}^{\mathrm{5}} =\frac{\mathrm{133}{x}−\mathrm{78}}{\mathrm{133}−\mathrm{78}{x}} \\ $$$$\mathrm{78}{x}^{\mathrm{6}} −\mathrm{133}{x}^{\mathrm{5}} +\mathrm{133}−\mathrm{78}=\mathrm{0} \\ $$$$\left({x}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{78}{x}^{\mathrm{4}} −\mathrm{133}{x}^{\mathrm{3}} +\mathrm{78}{x}^{\mathrm{2}} +\mathrm{78}−\mathrm{133}{x}\right. \\ $$$$\Rightarrow{let}\:{x}+\frac{\mathrm{1}}{{x}}={t},{then}\:{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }={t}^{\mathrm{2}} −\mathrm{2} \\ $$$$\mathrm{78}\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)\:−\mathrm{133}\left({x}+\frac{\mathrm{1}}{{x}}\right)+\mathrm{78}=\mathrm{0} \\ $$$$=\mathrm{78}\left({t}^{\mathrm{2}} −\mathrm{2}\right)−\mathrm{133}\left({t}\right)+\mathrm{78}=\mathrm{0} \\ $$$$=\mathrm{78}{t}^{\mathrm{2}} −\mathrm{133}{t}−\mathrm{78}=\mathrm{0} \\ $$$$\Rightarrow{t}=\frac{\mathrm{13}}{\mathrm{6}}{and}\:−\frac{\mathrm{6}}{\mathrm{13}} \\ $$$${when}\:{x}+\frac{\mathrm{1}}{{x}}=\frac{\mathrm{13}}{\mathrm{6}} \\ $$$${x}=\frac{\mathrm{2}}{\mathrm{3}},\frac{\mathrm{3}}{\mathrm{2}} \\ $$$${roots}\:{of}\:{the}\:{equation}\:{are}\:\mathrm{1},−\mathrm{1},\frac{\mathrm{2}}{\mathrm{3}},\frac{\mathrm{3}}{\mathrm{2}} \\ $$
