Question and Answers Forum

All Questions      Topic List

Vector Calculus Questions

Previous in All Question      Next in All Question      

Previous in Vector Calculus      Next in Vector Calculus      

Question Number 128282 by BHOOPENDRA last updated on 06/Jan/21

Answered by mr W last updated on 06/Jan/21

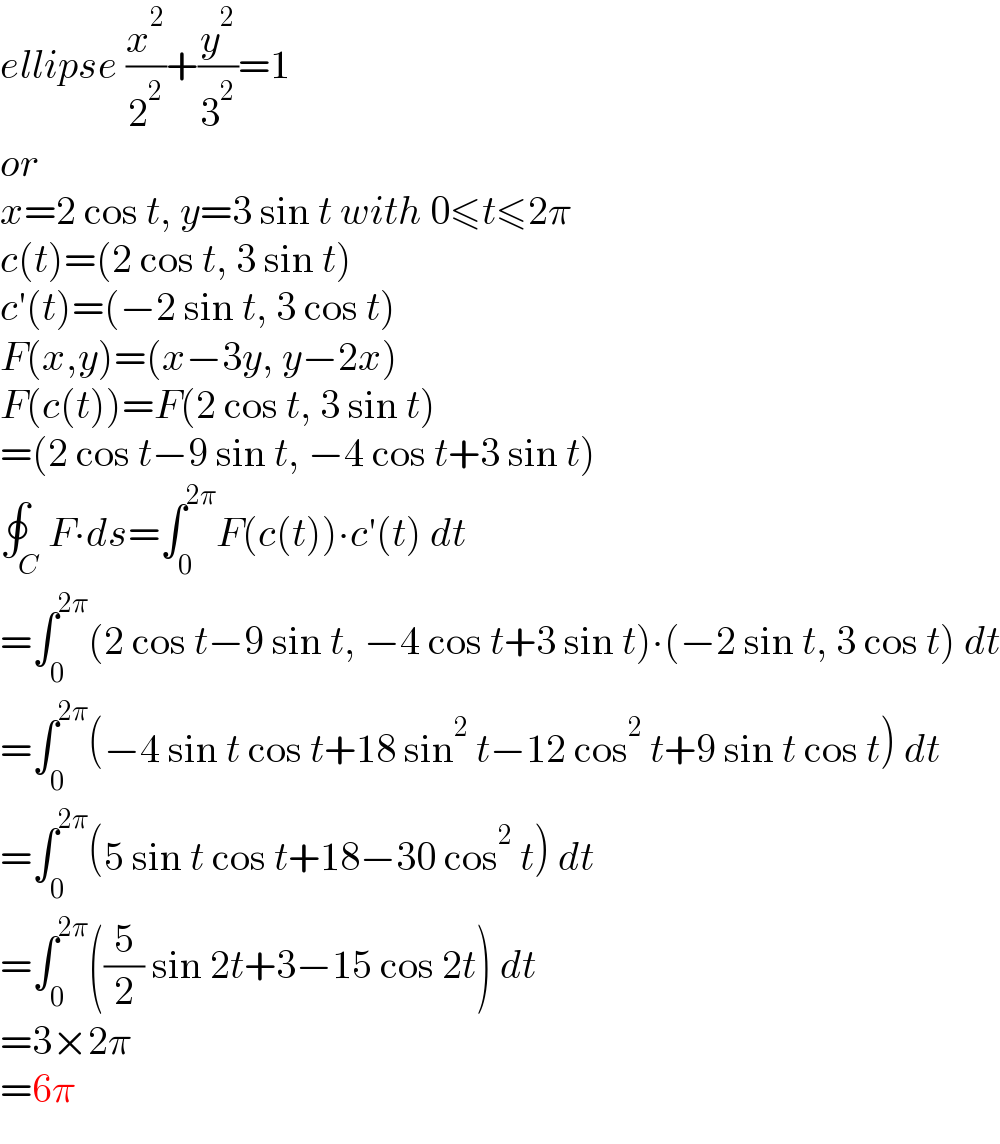
ellipse (x^2 /2^2 )+(y^2 /3^2 )=1 or x=2 cos t, y=3 sin t with 0≤t≤2π c(t)=(2 cos t, 3 sin t) c′(t)=(−2 sin t, 3 cos t) F(x,y)=(x−3y, y−2x) F(c(t))=F(2 cos t, 3 sin t) =(2 cos t−9 sin t, −4 cos t+3 sin t) ∮_C F∙ds=∫_0 ^(2π) F(c(t))∙c′(t) dt =∫_0 ^(2π) (2 cos t−9 sin t, −4 cos t+3 sin t)∙(−2 sin t, 3 cos t) dt =∫_0 ^(2π) (−4 sin t cos t+18 sin^2 t−12 cos^2 t+9 sin t cos t) dt =∫_0 ^(2π) (5 sin t cos t+18−30 cos^2 t) dt =∫_0 ^(2π) ((5/2) sin 2t+3−15 cos 2t) dt =3×2π =6π

$${ellipse}\:\frac{{x}^{\mathrm{2}} }{\mathrm{2}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{\mathrm{3}^{\mathrm{2}} }=\mathrm{1} \\ $$$${or} \\ $$$${x}=\mathrm{2}\:\mathrm{cos}\:{t},\:{y}=\mathrm{3}\:\mathrm{sin}\:{t}\:{with}\:\mathrm{0}\leqslant{t}\leqslant\mathrm{2}\pi \\ $$$${c}\left({t}\right)=\left(\mathrm{2}\:\mathrm{cos}\:{t},\:\mathrm{3}\:\mathrm{sin}\:{t}\right) \\ $$$${c}'\left({t}\right)=\left(−\mathrm{2}\:\mathrm{sin}\:{t},\:\mathrm{3}\:\mathrm{cos}\:{t}\right) \\ $$$${F}\left({x},{y}\right)=\left({x}−\mathrm{3}{y},\:{y}−\mathrm{2}{x}\right) \\ $$$${F}\left({c}\left({t}\right)\right)={F}\left(\mathrm{2}\:\mathrm{cos}\:{t},\:\mathrm{3}\:\mathrm{sin}\:{t}\right) \\ $$$$=\left(\mathrm{2}\:\mathrm{cos}\:{t}−\mathrm{9}\:\mathrm{sin}\:{t},\:−\mathrm{4}\:\mathrm{cos}\:{t}+\mathrm{3}\:\mathrm{sin}\:{t}\right) \\ $$$$\oint_{{C}} {F}\centerdot{ds}=\int_{\mathrm{0}} ^{\mathrm{2}\pi} {F}\left({c}\left({t}\right)\right)\centerdot{c}'\left({t}\right)\:{dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \left(\mathrm{2}\:\mathrm{cos}\:{t}−\mathrm{9}\:\mathrm{sin}\:{t},\:−\mathrm{4}\:\mathrm{cos}\:{t}+\mathrm{3}\:\mathrm{sin}\:{t}\right)\centerdot\left(−\mathrm{2}\:\mathrm{sin}\:{t},\:\mathrm{3}\:\mathrm{cos}\:{t}\right)\:{dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \left(−\mathrm{4}\:\mathrm{sin}\:{t}\:\mathrm{cos}\:{t}+\mathrm{18}\:\mathrm{sin}^{\mathrm{2}} \:{t}−\mathrm{12}\:\mathrm{cos}^{\mathrm{2}} \:{t}+\mathrm{9}\:\mathrm{sin}\:{t}\:\mathrm{cos}\:{t}\right)\:{dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \left(\mathrm{5}\:\mathrm{sin}\:{t}\:\mathrm{cos}\:{t}+\mathrm{18}−\mathrm{30}\:\mathrm{cos}^{\mathrm{2}} \:{t}\right)\:{dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \left(\frac{\mathrm{5}}{\mathrm{2}}\:\mathrm{sin}\:\mathrm{2}{t}+\mathrm{3}−\mathrm{15}\:\mathrm{cos}\:\mathrm{2}{t}\right)\:{dt} \\ $$$$=\mathrm{3}×\mathrm{2}\pi \\ $$$$=\mathrm{6}\pi \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com