
Question Number 128262 by Ahmed1hamouda last updated on 06/Jan/21
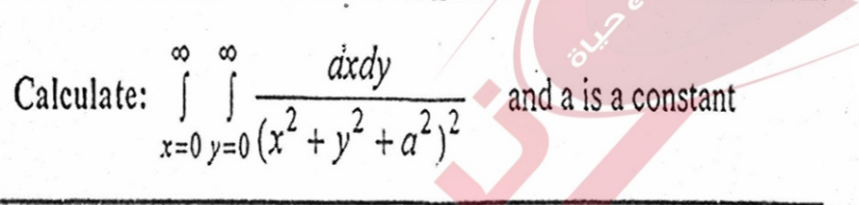
Answered by mr W last updated on 06/Jan/21
![∫_0 ^∞ ∫_0 ^∞ ((dxdy)/((x^2 +y^2 +a^2 )^2 )) =∫_0 ^∞ [∫_0 ^∞ (dx/((x^2 +y^2 +a^2 )^2 ))]dy =∫_0 ^∞ (1/(2(y^2 +a^2 )))[((tan^(−1) (x/( (√(y^2 +a^2 )))))/( (√(y^2 +a^2 ))))+(x/(x^2 +y^2 +a^2 ))]_0 ^∞ dy =∫_0 ^∞ (1/(2(y^2 +a^2 )))×(π/( 2(√(y^2 +a^2 ))))dy =(π/4)∫_0 ^∞ (dy/( (y^2 +a^2 )(√(y^2 +a^2 )))) =(π/(4a^2 ))[(y/( (√(y^2 +a^2 ))))]_0 ^∞ =(π/(4a^2 ))×lim_(y→∞) (1/( (√(1+(a^2 /y^2 ))))) =(π/(4a^2 ))](Q128306.png)
$$\int_{\mathrm{0}} ^{\infty} \int_{\mathrm{0}} ^{\infty} \frac{{dxdy}}{\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$=\int_{\mathrm{0}} ^{\infty} \left[\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)^{\mathrm{2}} }\right]{dy} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{2}\left({y}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)}\left[\frac{\mathrm{tan}^{−\mathrm{1}} \frac{{x}}{\:\sqrt{{y}^{\mathrm{2}} +{a}^{\mathrm{2}} }}}{\:\sqrt{{y}^{\mathrm{2}} +{a}^{\mathrm{2}} }}+\frac{{x}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{a}^{\mathrm{2}} }\right]_{\mathrm{0}} ^{\infty} {dy} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{2}\left({y}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)}×\frac{\pi}{\:\mathrm{2}\sqrt{{y}^{\mathrm{2}} +{a}^{\mathrm{2}} }}{dy} \\ $$$$=\frac{\pi}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \frac{{dy}}{\:\left({y}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)\sqrt{{y}^{\mathrm{2}} +{a}^{\mathrm{2}} }} \\ $$$$=\frac{\pi}{\mathrm{4}{a}^{\mathrm{2}} }\left[\frac{{y}}{\:\sqrt{{y}^{\mathrm{2}} +{a}^{\mathrm{2}} }}\right]_{\mathrm{0}} ^{\infty} \\ $$$$=\frac{\pi}{\mathrm{4}{a}^{\mathrm{2}} }×\underset{{y}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\frac{{a}^{\mathrm{2}} }{{y}^{\mathrm{2}} }}} \\ $$$$=\frac{\pi}{\mathrm{4}{a}^{\mathrm{2}} } \\ $$
Answered by mnjuly1970 last updated on 06/Jan/21
![x=rcos(θ) ⇒ ∣j(r,θ)=∣((∂(x,y))/(∂(r,θ)))∣=r y=rsin(θ) Ω=∫_0 ^(π/2) ∫_0 ^( ∞) (r/((r^2 +a^2 )^2 ))drdθ =∫_0 ^( (π/2)) [((−1)/(2(r^2 +a^2 )))]_0 ^∞ dθ=∫_0 ^( (π/2)) (1/(2a^2 ))dθ=(π/(4a^2 )) Ω=(π/(4a^2 )) ✓](Q128308.png)
$${x}={rcos}\left(\theta\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\mid{j}\left({r},\theta\right)=\mid\frac{\partial\left({x},{y}\right)}{\partial\left({r},\theta\right)}\mid={r} \\ $$$${y}={rsin}\left(\theta\right) \\ $$$$\Omega=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \int_{\mathrm{0}} ^{\:\infty} \frac{{r}}{\left({r}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)^{\mathrm{2}} }{drd}\theta \\ $$$$=\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \left[\frac{−\mathrm{1}}{\mathrm{2}\left({r}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)}\right]_{\mathrm{0}} ^{\infty} {d}\theta=\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{\mathrm{2}{a}^{\mathrm{2}} }{d}\theta=\frac{\pi}{\mathrm{4}{a}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Omega=\frac{\pi}{\mathrm{4}{a}^{\mathrm{2}} }\:\:\checkmark \\ $$
