
Question Number 128197 by BHOOPENDRA last updated on 05/Jan/21
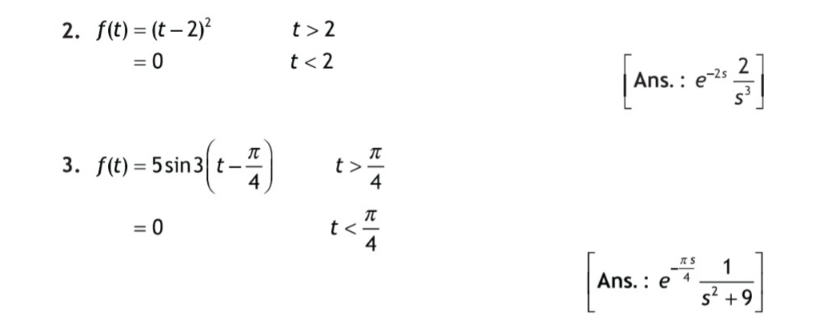
Commented by BHOOPENDRA last updated on 05/Jan/21
$${help}\:{me}\:{out}\:{this}? \\ $$
Answered by Dwaipayan Shikari last updated on 05/Jan/21
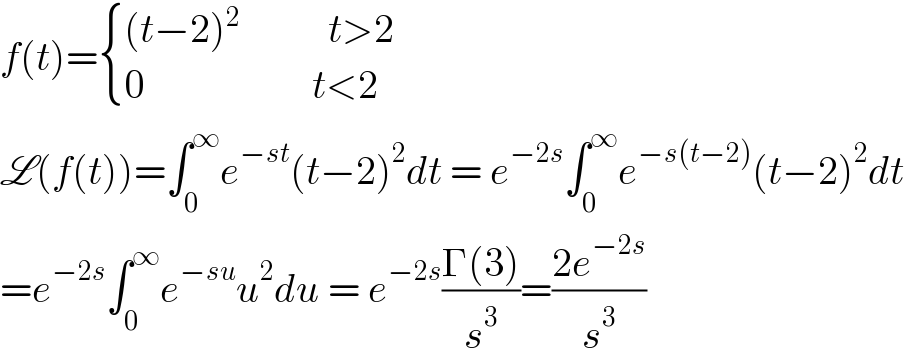
$${f}\left({t}\right)=\begin{cases}{\left({t}−\mathrm{2}\right)^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:\:{t}>\mathrm{2}}\\{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{t}<\mathrm{2}}\end{cases} \\ $$$$\mathscr{L}\left({f}\left({t}\right)\right)=\int_{\mathrm{0}} ^{\infty} {e}^{−{st}} \left({t}−\mathrm{2}\right)^{\mathrm{2}} {dt}\:=\:{e}^{−\mathrm{2}{s}} \int_{\mathrm{0}} ^{\infty} {e}^{−{s}\left({t}−\mathrm{2}\right)} \left({t}−\mathrm{2}\right)^{\mathrm{2}} {dt} \\ $$$$={e}^{−\mathrm{2}{s}} \int_{\mathrm{0}} ^{\infty} {e}^{−{su}} {u}^{\mathrm{2}} {du}\:=\:{e}^{−\mathrm{2}{s}} \frac{\Gamma\left(\mathrm{3}\right)}{{s}^{\mathrm{3}} }=\frac{\mathrm{2}{e}^{−\mathrm{2}{s}} }{{s}^{\mathrm{3}} } \\ $$
Commented by BHOOPENDRA last updated on 05/Jan/21
$${thanks}\:{sir}\:{n}\:{second}\:{one}? \\ $$
