Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 12814 by syambabu087@gmail.com last updated on 02/May/17

Commented by FilupS last updated on 02/May/17

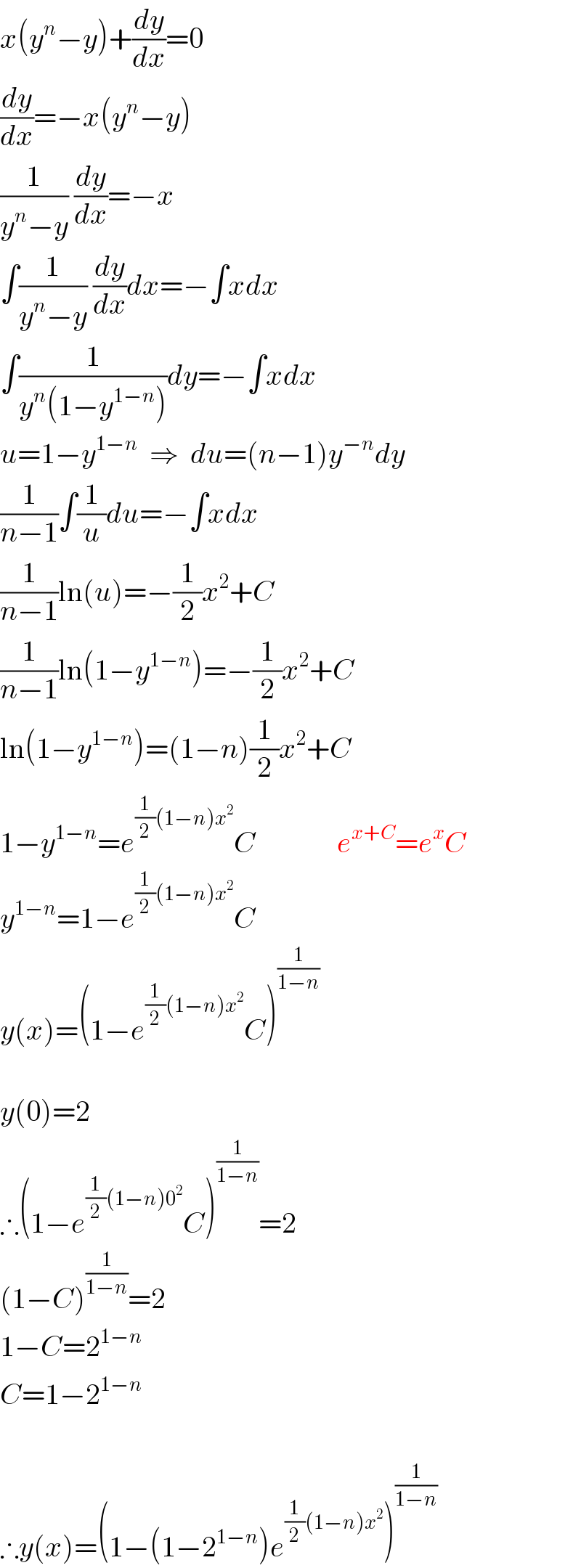
x(y^n −y)+(dy/dx)=0 (dy/dx)=−x(y^n −y) (1/(y^n −y)) (dy/dx)=−x ∫(1/(y^n −y)) (dy/dx)dx=−∫xdx ∫(1/(y^n (1−y^(1−n) )))dy=−∫xdx u=1−y^(1−n) ⇒ du=(n−1)y^(−n) dy (1/(n−1))∫(1/u)du=−∫xdx (1/(n−1))ln(u)=−(1/2)x^2 +C (1/(n−1))ln(1−y^(1−n) )=−(1/2)x^2 +C ln(1−y^(1−n) )=(1−n)(1/2)x^2 +C 1−y^(1−n) =e^((1/2)(1−n)x^2 ) C e^(x+C) =e^x C y^(1−n) =1−e^((1/2)(1−n)x^2 ) C y(x)=(1−e^((1/2)(1−n)x^2 ) C)^(1/(1−n)) y(0)=2 ∴(1−e^((1/2)(1−n)0^2 ) C)^(1/(1−n)) =2 (1−C)^(1/(1−n)) =2 1−C=2^(1−n) C=1−2^(1−n) ∴y(x)=(1−(1−2^(1−n) )e^((1/2)(1−n)x^2 ) )^(1/(1−n))

$${x}\left({y}^{{n}} −{y}\right)+\frac{{dy}}{{dx}}=\mathrm{0} \\ $$$$\frac{{dy}}{{dx}}=−{x}\left({y}^{{n}} −{y}\right) \\ $$$$\frac{\mathrm{1}}{{y}^{{n}} −{y}}\:\frac{{dy}}{{dx}}=−{x} \\ $$$$\int\frac{\mathrm{1}}{{y}^{{n}} −{y}}\:\frac{{dy}}{{dx}}{dx}=−\int{xdx} \\ $$$$\int\frac{\mathrm{1}}{{y}^{{n}} \left(\mathrm{1}−{y}^{\mathrm{1}−{n}} \right)}{dy}=−\int{xdx} \\ $$$${u}=\mathrm{1}−{y}^{\mathrm{1}−{n}} \:\:\Rightarrow\:\:{du}=\left({n}−\mathrm{1}\right){y}^{−{n}} {dy} \\ $$$$\frac{\mathrm{1}}{{n}−\mathrm{1}}\int\frac{\mathrm{1}}{{u}}{du}=−\int{xdx} \\ $$$$\frac{\mathrm{1}}{{n}−\mathrm{1}}\mathrm{ln}\left({u}\right)=−\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} +{C} \\ $$$$\frac{\mathrm{1}}{{n}−\mathrm{1}}\mathrm{ln}\left(\mathrm{1}−{y}^{\mathrm{1}−{n}} \right)=−\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} +{C} \\ $$$$\mathrm{ln}\left(\mathrm{1}−{y}^{\mathrm{1}−{n}} \right)=\left(\mathrm{1}−{n}\right)\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} +{C} \\ $$$$\mathrm{1}−{y}^{\mathrm{1}−{n}} ={e}^{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−{n}\right){x}^{\mathrm{2}} } {C}\:\:\:\:\:\:\:\:\:\:\:\:\:\:{e}^{{x}+{C}} ={e}^{{x}} {C} \\ $$$${y}^{\mathrm{1}−{n}} =\mathrm{1}−{e}^{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−{n}\right){x}^{\mathrm{2}} } {C} \\ $$$${y}\left({x}\right)=\left(\mathrm{1}−{e}^{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−{n}\right){x}^{\mathrm{2}} } {C}\right)^{\frac{\mathrm{1}}{\mathrm{1}−{n}}} \\ $$$$\: \\ $$$${y}\left(\mathrm{0}\right)=\mathrm{2} \\ $$$$\therefore\left(\mathrm{1}−{e}^{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−{n}\right)\mathrm{0}^{\mathrm{2}} } {C}\right)^{\frac{\mathrm{1}}{\mathrm{1}−{n}}} =\mathrm{2} \\ $$$$\left(\mathrm{1}−{C}\right)^{\frac{\mathrm{1}}{\mathrm{1}−{n}}} =\mathrm{2} \\ $$$$\mathrm{1}−{C}=\mathrm{2}^{\mathrm{1}−{n}} \\ $$$${C}=\mathrm{1}−\mathrm{2}^{\mathrm{1}−{n}} \\ $$$$\: \\ $$$$\therefore{y}\left({x}\right)=\left(\mathrm{1}−\left(\mathrm{1}−\mathrm{2}^{\mathrm{1}−{n}} \right){e}^{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−{n}\right){x}^{\mathrm{2}} } \right)^{\frac{\mathrm{1}}{\mathrm{1}−{n}}} \\ $$

Commented by mrW1 last updated on 02/May/17

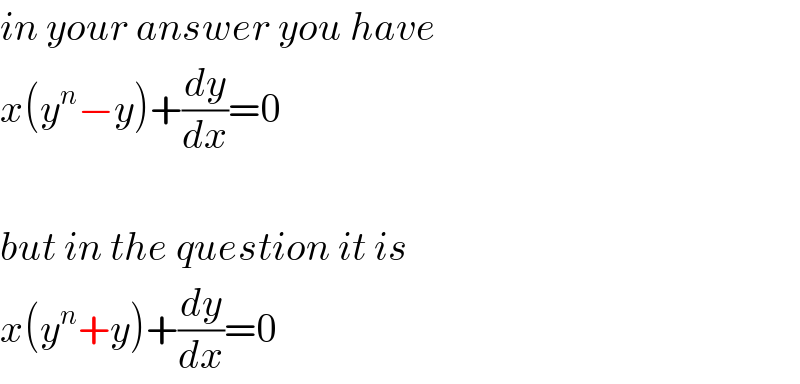
in your answer you have x(y^n −y)+(dy/dx)=0 but in the question it is x(y^n +y)+(dy/dx)=0

$${in}\:{your}\:{answer}\:{you}\:{have} \\ $$$${x}\left({y}^{{n}} −{y}\right)+\frac{{dy}}{{dx}}=\mathrm{0} \\ $$$$ \\ $$$${but}\:{in}\:{the}\:{question}\:{it}\:{is} \\ $$$${x}\left({y}^{{n}} +{y}\right)+\frac{{dy}}{{dx}}=\mathrm{0} \\ $$

Answered by sma3l2996 last updated on 03/May/17

(y^n +y)x=−(dy/dx)⇔−xdx=(dy/(y^n +y)) ((−1)/2)x^2 +c=∫(dy/(y(y^(n−1) +1))) u=(1/(y^(n−1) +1))⇒du=((−(n−1)y^(n−2) )/((1+y^(n−1) )^2 ))dy=−(((n−1)y^(n−1) )/(y(y^(n−1) +1)^2 ))dy y^(n−1) =−((u−1)/u) du=(((n−1)×u)/(y(y^(n−1) +1)))×((u−1)/u)dy=(n−1)((u−1)/(y(y^(n−1) +1)))dy (dy/(y(y^(n−1) +1)))=(du/((n−1)(u−1))) ((−1)/2)x^2 +c=(1/(n−1))∫(du/(u−1))=(1/(n−1))ln(u−1)+a −(1/2)x^2 +c_1 =(1/(n−1))ln((1/(y^(n−1) +1))−1) (1/(y^(n−1) +1))−1=e^(−((n−1)/2)x^2 +(n−1)c_1 ) =C×e^(−((n−1)/2)x^2 ) (y^(n−1) +1)(C×e^(−((n−1)/2)x^2 ) +1)=1 y^(n−1) =(1/(C×e^(−((n−1)/2)x^2 ) +1))−1=−((C×e^(−((n−1)/2)x^2 ) )/(C×e^(−((n−1)/2)x^2 ) +1)) y(0)=2 −(C/(C+1))=2^(n−1) ⇔C=−(2^(n−1) /(2^(n−1) +1)) y^(n−1) =−(C/(e^(((n−1)/2)x^2 ) (C×e^(−((n−1)/2)x^2 ) +1))) =(2^(n−1) /((2^(n−1) +1)e^(((n−1)/2)x^2 ) (((−2^(n−1) )/((2^(n−1) +1)e^(((n−1)/2)x^2 ) ))+1)))=(2^(n−1) /((2^(n−1) +1)e^(((n−1)/2)x^2 ) −2^(n−1) )) y(x)=(2/(((2^(n−1) +1)e^(((n−1)/2)x^2 ) −2^(n−1) )^(1/(n−1)) ))

$$\left({y}^{{n}} +{y}\right){x}=−\frac{{dy}}{{dx}}\Leftrightarrow−{xdx}=\frac{{dy}}{{y}^{{n}} +{y}} \\ $$$$\frac{−\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} +{c}=\int\frac{{dy}}{{y}\left({y}^{{n}−\mathrm{1}} +\mathrm{1}\right)} \\ $$$${u}=\frac{\mathrm{1}}{{y}^{{n}−\mathrm{1}} +\mathrm{1}}\Rightarrow{du}=\frac{−\left({n}−\mathrm{1}\right){y}^{{n}−\mathrm{2}} }{\left(\mathrm{1}+{y}^{{n}−\mathrm{1}} \right)^{\mathrm{2}} }{dy}=−\frac{\left({n}−\mathrm{1}\right){y}^{{n}−\mathrm{1}} }{{y}\left({y}^{{n}−\mathrm{1}} +\mathrm{1}\right)^{\mathrm{2}} }{dy} \\ $$$${y}^{{n}−\mathrm{1}} =−\frac{{u}−\mathrm{1}}{{u}} \\ $$$${du}=\frac{\left({n}−\mathrm{1}\right)×{u}}{{y}\left({y}^{{n}−\mathrm{1}} +\mathrm{1}\right)}×\frac{{u}−\mathrm{1}}{{u}}{dy}=\left({n}−\mathrm{1}\right)\frac{{u}−\mathrm{1}}{{y}\left({y}^{{n}−\mathrm{1}} +\mathrm{1}\right)}{dy} \\ $$$$\frac{{dy}}{{y}\left({y}^{{n}−\mathrm{1}} +\mathrm{1}\right)}=\frac{{du}}{\left({n}−\mathrm{1}\right)\left({u}−\mathrm{1}\right)} \\ $$$$\frac{−\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} +{c}=\frac{\mathrm{1}}{{n}−\mathrm{1}}\int\frac{{du}}{{u}−\mathrm{1}}=\frac{\mathrm{1}}{{n}−\mathrm{1}}{ln}\left({u}−\mathrm{1}\right)+{a} \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} +{c}_{\mathrm{1}} =\frac{\mathrm{1}}{{n}−\mathrm{1}}{ln}\left(\frac{\mathrm{1}}{{y}^{{n}−\mathrm{1}} +\mathrm{1}}−\mathrm{1}\right) \\ $$$$\frac{\mathrm{1}}{{y}^{{n}−\mathrm{1}} +\mathrm{1}}−\mathrm{1}={e}^{−\frac{{n}−\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} +\left({n}−\mathrm{1}\right){c}_{\mathrm{1}} } ={C}×{e}^{−\frac{{n}−\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} } \\ $$$$\left({y}^{{n}−\mathrm{1}} +\mathrm{1}\right)\left({C}×{e}^{−\frac{{n}−\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} } +\mathrm{1}\right)=\mathrm{1} \\ $$$${y}^{{n}−\mathrm{1}} =\frac{\mathrm{1}}{{C}×{e}^{−\frac{{n}−\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} } +\mathrm{1}}−\mathrm{1}=−\frac{{C}×{e}^{−\frac{{n}−\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} } }{{C}×{e}^{−\frac{{n}−\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} } +\mathrm{1}} \\ $$$${y}\left(\mathrm{0}\right)=\mathrm{2}\:\: \\ $$$$−\frac{{C}}{{C}+\mathrm{1}}=\mathrm{2}^{{n}−\mathrm{1}} \Leftrightarrow{C}=−\frac{\mathrm{2}^{{n}−\mathrm{1}} }{\mathrm{2}^{{n}−\mathrm{1}} +\mathrm{1}} \\ $$$${y}^{{n}−\mathrm{1}} =−\frac{{C}}{{e}^{\frac{{n}−\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} } \left({C}×{e}^{−\frac{{n}−\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} } +\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{2}^{{n}−\mathrm{1}} }{\left(\mathrm{2}^{{n}−\mathrm{1}} +\mathrm{1}\right){e}^{\frac{{n}−\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} } \left(\frac{−\mathrm{2}^{{n}−\mathrm{1}} }{\left(\mathrm{2}^{{n}−\mathrm{1}} +\mathrm{1}\right){e}^{\frac{{n}−\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} } }+\mathrm{1}\right)}=\frac{\mathrm{2}^{{n}−\mathrm{1}} }{\left(\mathrm{2}^{{n}−\mathrm{1}} +\mathrm{1}\right){e}^{\frac{{n}−\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} } −\mathrm{2}^{{n}−\mathrm{1}} } \\ $$$${y}\left({x}\right)=\frac{\mathrm{2}}{\left(\left(\mathrm{2}^{{n}−\mathrm{1}} +\mathrm{1}\right){e}^{\frac{{n}−\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} } −\mathrm{2}^{{n}−\mathrm{1}} \right)^{\frac{\mathrm{1}}{{n}−\mathrm{1}}} } \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com