
Question Number 128015 by Algoritm last updated on 03/Jan/21
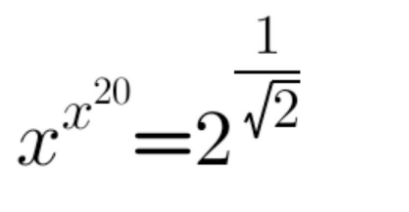
Answered by MJS_new last updated on 03/Jan/21

$${x}=\sqrt[{\mathrm{8}}]{\mathrm{2}} \\ $$
Answered by MJS_new last updated on 03/Jan/21
![x^x^(20) =2^(1/( (√2))) let x=2^r [obviously only 2^k −factors on the rhs] 2^(2^(20r) r) =2^(1/( (√2))) 2^(20r) r=(1/( (√2)))=2^(−(1/2)) again only 2^k −factors ⇒ r=2^(−n) now try n=1, 2, 3, ... ⇒ n=3 ⇒ r=(1/8) ⇒ x=(2)^(1/8)](Q128022.png)
$${x}^{{x}^{\mathrm{20}} } =\mathrm{2}^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} \\ $$$$\mathrm{let}\:{x}=\mathrm{2}^{{r}} \:\left[\mathrm{obviously}\:\mathrm{only}\:\mathrm{2}^{{k}} −\mathrm{factors}\:\mathrm{on}\:\mathrm{the}\:\mathrm{rhs}\right] \\ $$$$\mathrm{2}^{\mathrm{2}^{\mathrm{20}{r}} {r}} =\mathrm{2}^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} \\ $$$$\mathrm{2}^{\mathrm{20}{r}} {r}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}=\mathrm{2}^{−\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\mathrm{again}\:\mathrm{only}\:\mathrm{2}^{{k}} −\mathrm{factors}\:\Rightarrow\:{r}=\mathrm{2}^{−{n}} \\ $$$$\mathrm{now}\:\mathrm{try}\:{n}=\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:... \\ $$$$\Rightarrow\:{n}=\mathrm{3}\:\Rightarrow\:{r}=\frac{\mathrm{1}}{\mathrm{8}}\:\Rightarrow\:{x}=\sqrt[{\mathrm{8}}]{\mathrm{2}} \\ $$
