
Question Number 127833 by Algoritm last updated on 02/Jan/21
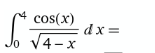
Answered by mathmax by abdo last updated on 02/Jan/21
![I =∫_0 ^4 ((cosx)/( (√(4−x))))dx we do the changement (√(4−x))=t ⇒4−x=t^2 I =∫_2 ^0 ((cos(4−t^2 ))/t)(−2t)dt =2∫_0 ^2 cos(4−t^2 )dt =2∫_0 ^2 (cos4 cost^2 +sin4 sint^2 )dt =2cos4 ∫_0 ^2 cos(t^2 )dt +2sin4 ∫_0 ^2 sin(t^2 )dt we have cosu=Σ_(n=0) ^∞ (((−1)^n u^(2n) )/((2n)!)) and sinu=Σ_(n=0) ^∞ (((−1)^n u^(2n+1) )/((2n+1)!)) ⇒ I =2cos4 ∫_0 ^2 Σ_(n=0) ^∞ (((−1)^n t^(2n) )/((2n)!))dt +2sin4 ∫_0 ^2 Σ_(n=0) ^∞ (((−1)^n t^(2n+1) )/((2n+1)!))dt =2cos4 Σ_(n=0) ^∞ (((−1)^n )/((2n)!))[(t^(2n+1) /(2n+1))]_0 ^2 +2sin4 Σ_(n=0) ^∞ (((−1)^n )/((2n+1)!))[(t^(2n+2) /(2n+2))]_0 ^2 =2cos4 Σ_(n=0) ^∞ (((−1)^n 2^(2n+1) )/((2n+1)(2n)!)) +2sin4 Σ_(n=0) ^∞ (((−1)^n 2^(2n+2) )/((2n+2)(2n+1)!))](Q127844.png)
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{4}} \:\frac{\mathrm{cosx}}{\:\sqrt{\mathrm{4}−\mathrm{x}}}\mathrm{dx}\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\sqrt{\mathrm{4}−\mathrm{x}}=\mathrm{t}\:\Rightarrow\mathrm{4}−\mathrm{x}=\mathrm{t}^{\mathrm{2}} \\ $$$$\mathrm{I}\:=\int_{\mathrm{2}} ^{\mathrm{0}} \:\frac{\mathrm{cos}\left(\mathrm{4}−\mathrm{t}^{\mathrm{2}} \right)}{\mathrm{t}}\left(−\mathrm{2t}\right)\mathrm{dt}\:=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{2}} \:\mathrm{cos}\left(\mathrm{4}−\mathrm{t}^{\mathrm{2}} \right)\mathrm{dt} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{2}} \left(\mathrm{cos4}\:\mathrm{cost}^{\mathrm{2}} +\mathrm{sin4}\:\mathrm{sint}^{\mathrm{2}} \right)\mathrm{dt} \\ $$$$=\mathrm{2cos4}\:\int_{\mathrm{0}} ^{\mathrm{2}} \:\mathrm{cos}\left(\mathrm{t}^{\mathrm{2}} \right)\mathrm{dt}\:+\mathrm{2sin4}\:\int_{\mathrm{0}} ^{\mathrm{2}} \:\mathrm{sin}\left(\mathrm{t}^{\mathrm{2}} \right)\mathrm{dt}\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{cosu}=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{u}^{\mathrm{2n}} }{\left(\mathrm{2n}\right)!} \\ $$$$\mathrm{and}\:\mathrm{sinu}=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{u}^{\mathrm{2n}+\mathrm{1}} }{\left(\mathrm{2n}+\mathrm{1}\right)!}\:\Rightarrow \\ $$$$\mathrm{I}\:=\mathrm{2cos4}\:\int_{\mathrm{0}} ^{\mathrm{2}} \sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{t}^{\mathrm{2n}} }{\left(\mathrm{2n}\right)!}\mathrm{dt}\:+\mathrm{2sin4}\:\int_{\mathrm{0}} ^{\mathrm{2}} \:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{t}^{\mathrm{2n}+\mathrm{1}} }{\left(\mathrm{2n}+\mathrm{1}\right)!}\mathrm{dt} \\ $$$$=\mathrm{2cos4}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}\right)!}\left[\frac{\mathrm{t}^{\mathrm{2n}+\mathrm{1}} }{\mathrm{2n}+\mathrm{1}}\right]_{\mathrm{0}} ^{\mathrm{2}} \:+\mathrm{2sin4}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)!}\left[\frac{\mathrm{t}^{\mathrm{2n}+\mathrm{2}} }{\mathrm{2n}+\mathrm{2}}\right]_{\mathrm{0}} ^{\mathrm{2}} \\ $$$$=\mathrm{2cos4}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{2}^{\mathrm{2n}+\mathrm{1}} }{\left(\mathrm{2n}+\mathrm{1}\right)\left(\mathrm{2n}\right)!}\:+\mathrm{2sin4}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{2}^{\mathrm{2n}+\mathrm{2}} }{\left(\mathrm{2n}+\mathrm{2}\right)\left(\mathrm{2n}+\mathrm{1}\right)!} \\ $$
Answered by Bird last updated on 02/Jan/21
![let determine approximate vslue of I we have cosu=1−(u^2 /2)+(u^4 /(4!))−... ⇒ 1−(u^2 /2)≤cosu ≤1−(u^2 /2)+(u^4 /(4!)) ⇒ ((1−(x^2 /2))/( (√(4−x))))≤((cosx)/( (√(4−x))))≤((1−(u^2 /2)+(u^4 /(4!)))/( (√(4−x)))) ⇒ ∫_0 ^4 ((1/( (√(4−x))))−(x^2 /( (√(4−x)))))dx≤I ≤ ∫_0 ^4 (1/( (√(4−x))))−∫_0 ^(4 ) (x^2 /(2(√(4−x))))dx+∫_0 ^4 (x^4 /(4!(√(4−x))))dx we have ∫_0 ^4 (dx/( (√(4−x))))=[−2(√(4−x))]_0 ^4 =4 ∫_0 ^4 (x^2 /(2(√(4−x))))dx =_(4−x=t^2 ) ∫_2 ^0 (((4−t^2 )^2 )/(2t))(−2t)dt =∫_0 ^2 (t^4 −8t^2 +16)dt =[(t^5 /5)−(8/3)t^3 +16t]_0 ^(2 ) =(2^5 /5)−((64)/3)+32=... ∫_0 ^4 (x^4 /(4!(√(4−x))))dx =_(4−x=t^2 ) ∫_2 ^0 (((4−t^2 )^4 )/(4!t))(−2t)dt =(2/(4!))∫_0 ^2 (t^4 −8t^(2 ) +16)^(2 ) dt =(2/(4!))∫_0 ^2 ((t^4 −8t^2 )^2 +32(t^4 −8t^2 )+16^2 )dt=... rest to collect the vslues...](Q127850.png)
$${let}\:{determine}\:{approximate}\:{vslue}\:{of}\:{I} \\ $$$${we}\:{have}\:{cosu}=\mathrm{1}−\frac{{u}^{\mathrm{2}} }{\mathrm{2}}+\frac{{u}^{\mathrm{4}} }{\mathrm{4}!}−...\:\Rightarrow \\ $$$$\mathrm{1}−\frac{{u}^{\mathrm{2}} }{\mathrm{2}}\leqslant{cosu}\:\leqslant\mathrm{1}−\frac{{u}^{\mathrm{2}} }{\mathrm{2}}+\frac{{u}^{\mathrm{4}} }{\mathrm{4}!}\:\Rightarrow \\ $$$$\frac{\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}}{\:\sqrt{\mathrm{4}−{x}}}\leqslant\frac{{cosx}}{\:\sqrt{\mathrm{4}−{x}}}\leqslant\frac{\mathrm{1}−\frac{{u}^{\mathrm{2}} }{\mathrm{2}}+\frac{{u}^{\mathrm{4}} }{\mathrm{4}!}}{\:\sqrt{\mathrm{4}−{x}}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{4}} \left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{4}−{x}}}−\frac{{x}^{\mathrm{2}} }{\:\sqrt{\mathrm{4}−{x}}}\right){dx}\leqslant{I}\:\leqslant \\ $$$$\int_{\mathrm{0}} ^{\mathrm{4}} \:\frac{\mathrm{1}}{\:\sqrt{\mathrm{4}−{x}}}−\int_{\mathrm{0}} ^{\mathrm{4}\:} \:\frac{{x}^{\mathrm{2}} }{\mathrm{2}\sqrt{\mathrm{4}−{x}}}{dx}+\int_{\mathrm{0}} ^{\mathrm{4}} \:\frac{{x}^{\mathrm{4}} }{\mathrm{4}!\sqrt{\mathrm{4}−{x}}}{dx} \\ $$$${we}\:{have}\:\int_{\mathrm{0}} ^{\mathrm{4}} \:\frac{{dx}}{\:\sqrt{\mathrm{4}−{x}}}=\left[−\mathrm{2}\sqrt{\mathrm{4}−{x}}\right]_{\mathrm{0}} ^{\mathrm{4}} \\ $$$$=\mathrm{4} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{4}} \:\:\:\frac{{x}^{\mathrm{2}} }{\mathrm{2}\sqrt{\mathrm{4}−{x}}}{dx}\:=_{\mathrm{4}−{x}={t}^{\mathrm{2}} } \:\:\int_{\mathrm{2}} ^{\mathrm{0}} \:\frac{\left(\mathrm{4}−{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{2}{t}}\left(−\mathrm{2}{t}\right){dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}} \left({t}^{\mathrm{4}} −\mathrm{8}{t}^{\mathrm{2}} \:+\mathrm{16}\right){dt} \\ $$$$=\left[\frac{{t}^{\mathrm{5}} }{\mathrm{5}}−\frac{\mathrm{8}}{\mathrm{3}}{t}^{\mathrm{3}} \:+\mathrm{16}{t}\right]_{\mathrm{0}} ^{\mathrm{2}\:} =\frac{\mathrm{2}^{\mathrm{5}} }{\mathrm{5}}−\frac{\mathrm{64}}{\mathrm{3}}+\mathrm{32}=... \\ $$$$\int_{\mathrm{0}} ^{\mathrm{4}} \:\:\frac{{x}^{\mathrm{4}} }{\mathrm{4}!\sqrt{\mathrm{4}−{x}}}{dx}\:=_{\mathrm{4}−{x}={t}^{\mathrm{2}} } \\ $$$$\int_{\mathrm{2}} ^{\mathrm{0}} \:\:\frac{\left(\mathrm{4}−{t}^{\mathrm{2}} \right)^{\mathrm{4}} }{\mathrm{4}!{t}}\left(−\mathrm{2}{t}\right){dt} \\ $$$$=\frac{\mathrm{2}}{\mathrm{4}!}\int_{\mathrm{0}} ^{\mathrm{2}} \left({t}^{\mathrm{4}} −\mathrm{8}{t}^{\mathrm{2}\:} +\mathrm{16}\right)^{\mathrm{2}\:} {dt} \\ $$$$=\frac{\mathrm{2}}{\mathrm{4}!}\int_{\mathrm{0}} ^{\mathrm{2}} \left(\left({t}^{\mathrm{4}} −\mathrm{8}{t}^{\mathrm{2}} \right)^{\mathrm{2}} \:+\mathrm{32}\left({t}^{\mathrm{4}} −\mathrm{8}{t}^{\mathrm{2}} \right)+\mathrm{16}^{\mathrm{2}} \right){dt}=... \\ $$$${rest}\:{to}\:{collect}\:{the}\:{vslues}... \\ $$
