
Question Number 127641 by Study last updated on 31/Dec/20

Answered by Dwaipayan Shikari last updated on 31/Dec/20
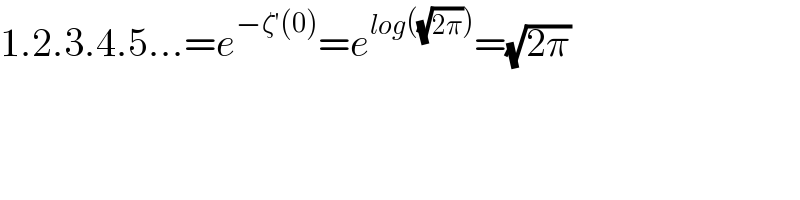
$$\mathrm{1}.\mathrm{2}.\mathrm{3}.\mathrm{4}.\mathrm{5}...={e}^{−\zeta'\left(\mathrm{0}\right)} ={e}^{{log}\left(\sqrt{\mathrm{2}\pi}\right)} =\sqrt{\mathrm{2}\pi} \\ $$
Commented by MJS_new last updated on 31/Dec/20
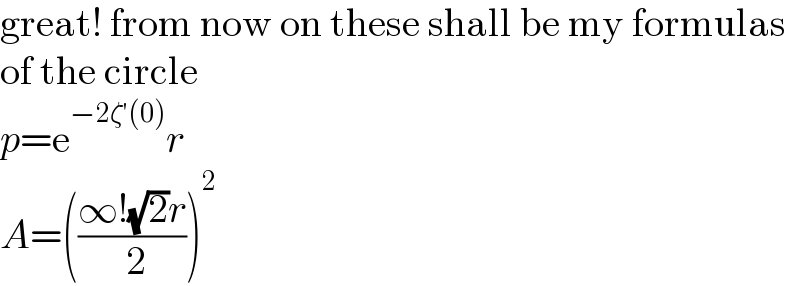
$$\mathrm{great}!\:\mathrm{from}\:\mathrm{now}\:\mathrm{on}\:\mathrm{these}\:\mathrm{shall}\:\mathrm{be}\:\mathrm{my}\:\mathrm{formulas} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{circle} \\ $$$${p}=\mathrm{e}^{−\mathrm{2}\zeta'\left(\mathrm{0}\right)} {r} \\ $$$${A}=\left(\frac{\infty!\sqrt{\mathrm{2}}{r}}{\:\mathrm{2}}\right)^{\mathrm{2}} \\ $$
Commented by Dwaipayan Shikari last updated on 31/Dec/20
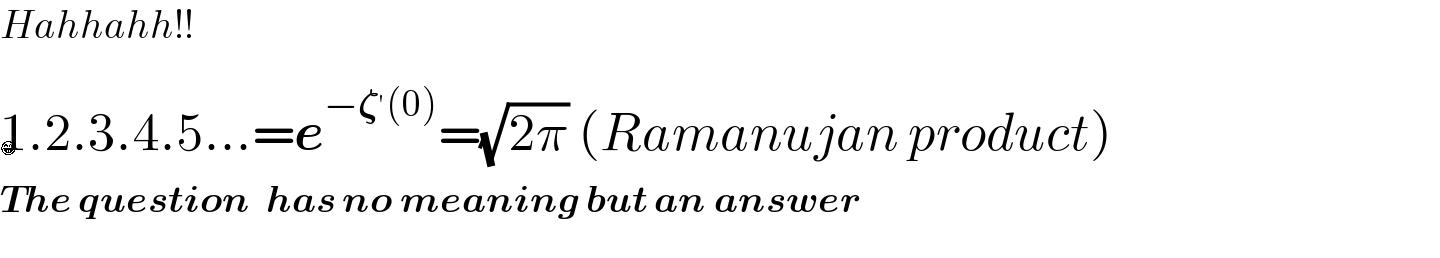
$${Hahhahh}!! \\ $$$$\mathrm{1}.\mathrm{2}.\mathrm{3}.\mathrm{4}.\mathrm{5}...=\boldsymbol{{e}}^{−\boldsymbol{\zeta}^{'} \left(\mathrm{0}\right)} =\sqrt{\mathrm{2}\pi}\:\left({Ramanujan}\:{product}\right) \\ $$$$\boldsymbol{{The}}\:\boldsymbol{{question}}\:\:\boldsymbol{{has}}\:\boldsymbol{{no}}\:\boldsymbol{{meaning}}\:\boldsymbol{{but}}\:\boldsymbol{{an}}\:\boldsymbol{{answer}} \\ $$$$ \\ $$😁
Commented by Dwaipayan Shikari last updated on 31/Dec/20

$$\boldsymbol{\mathcal{A}}=\left(\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)!{r}\right)^{\mathrm{2}} \\ $$
Commented by MJS_new last updated on 31/Dec/20

$${yes} \\ $$
Commented by Study last updated on 31/Dec/20
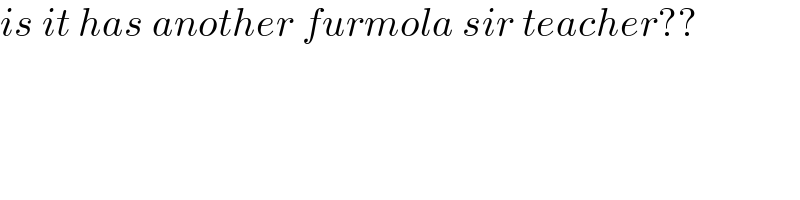
$${is}\:{it}\:{has}\:{another}\:{furmola}\:{sir}\:{teacher}?? \\ $$
Commented by Dwaipayan Shikari last updated on 31/Dec/20
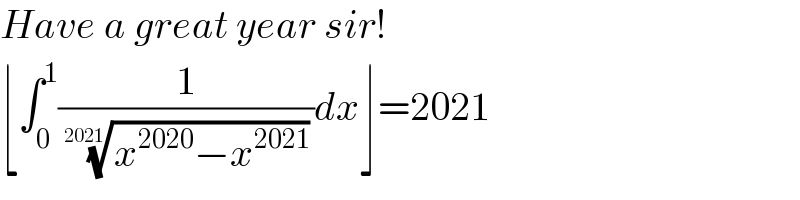
$${Have}\:{a}\:{great}\:{year}\:{sir}! \\ $$$$\lfloor\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt[{\mathrm{2021}}]{{x}^{\mathrm{2020}} −{x}^{\mathrm{2021}} }}{dx}\rfloor=\mathrm{2021} \\ $$
Commented by Study last updated on 01/Jan/21
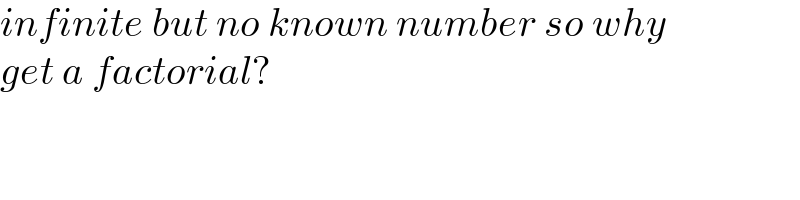
$${infinite}\:{but}\:{no}\:{known}\:{number}\:{so}\:{why} \\ $$$${get}\:{a}\:{factorial}? \\ $$
Commented by Study last updated on 02/Jan/21

$$????? \\ $$
