Question and Answers Forum

All Questions      Topic List

Coordinate Geometry Questions

Previous in All Question      Next in All Question      

Previous in Coordinate Geometry      Next in Coordinate Geometry      

Question Number 127127 by mr W last updated on 27/Dec/20

Commented by mr W last updated on 27/Dec/20

This question was once asked. Find the radius of circle in terms of parameters a and b of the ellipse.

$${This}\:{question}\:{was}\:{once}\:{asked}. \\ $$$$ \\ $$$${Find}\:{the}\:{radius}\:{of}\:{circle}\:{in}\:{terms}\:{of} \\ $$$${parameters}\:{a}\:{and}\:{b}\:{of}\:{the}\:{ellipse}. \\ $$

Commented by PRITHWISH SEN 2 last updated on 27/Dec/20

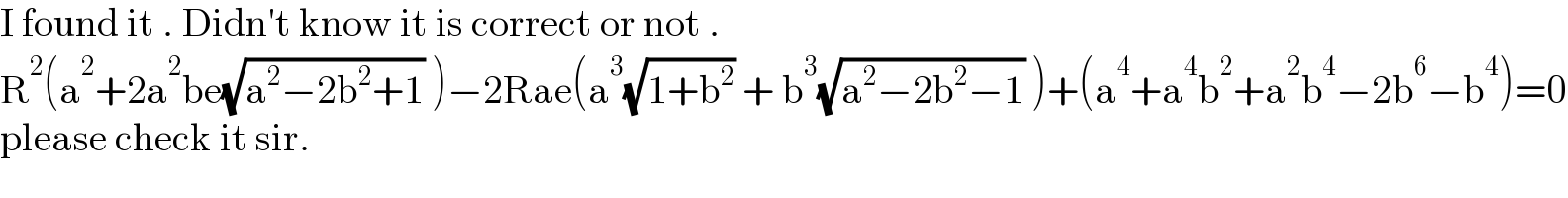
I found it . Didn′t know it is correct or not . R^2 (a^2 +2a^2 be(√(a^2 −2b^2 +1)) )−2Rae(a^3 (√(1+b^2 )) + b^3 (√(a^2 −2b^2 −1)) )+(a^4 +a^4 b^2 +a^2 b^4 −2b^6 −b^4 )=0 please check it sir.

$$\mathrm{I}\:\mathrm{found}\:\mathrm{it}\:.\:\mathrm{Didn}'\mathrm{t}\:\mathrm{know}\:\mathrm{it}\:\mathrm{is}\:\mathrm{correct}\:\mathrm{or}\:\mathrm{not}\:. \\ $$$$\mathrm{R}^{\mathrm{2}} \left(\mathrm{a}^{\mathrm{2}} +\mathrm{2a}^{\mathrm{2}} \mathrm{be}\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{2b}^{\mathrm{2}} +\mathrm{1}}\:\right)−\mathrm{2Rae}\left(\mathrm{a}^{\mathrm{3}} \sqrt{\mathrm{1}+\mathrm{b}^{\mathrm{2}} }\:+\:\mathrm{b}^{\mathrm{3}} \sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{2b}^{\mathrm{2}} −\mathrm{1}}\:\right)+\left(\mathrm{a}^{\mathrm{4}} +\mathrm{a}^{\mathrm{4}} \mathrm{b}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} \mathrm{b}^{\mathrm{4}} −\mathrm{2b}^{\mathrm{6}} −\mathrm{b}^{\mathrm{4}} \right)=\mathrm{0} \\ $$$$\mathrm{please}\:\mathrm{check}\:\mathrm{it}\:\mathrm{sir}. \\ $$

Commented by mr W last updated on 27/Dec/20

what is e in your equation? i can′t check your solution. please show your working sir! i didn′t think it is possible to get a quadratic equation for R, but it′s great when you have found a way.

$${what}\:{is}\:{e}\:{in}\:{your}\:{equation}? \\ $$$${i}\:{can}'{t}\:{check}\:{your}\:{solution}.\:{please} \\ $$$${show}\:{your}\:{working}\:{sir}! \\ $$$${i}\:{didn}'{t}\:{think}\:{it}\:{is}\:{possible}\:{to}\:{get}\:{a} \\ $$$${quadratic}\:{equation}\:{for}\:{R},\:{but}\:{it}'{s} \\ $$$${great}\:{when}\:{you}\:{have}\:{found}\:{a}\:{way}. \\ $$

Commented by PRITHWISH SEN 2 last updated on 27/Dec/20

ok sir i will post it later.e is ecentricity.

$$\mathrm{ok}\:\mathrm{sir}\:\mathrm{i}\:\mathrm{will}\:\mathrm{post}\:\mathrm{it}\:\mathrm{later}.\mathrm{e}\:\mathrm{is}\:\mathrm{ecentricity}. \\ $$

Commented by ajfour last updated on 27/Dec/20

Commented by ajfour last updated on 30/Dec/20

A Point of ellipse (acos ψ,bsin ψ) let s is distance of this point from center of circle. s^2 =(R−acos ψ)^2 +(R−bsin ψ)^2 s_(min) =R ...(i) s^2 =2R^2 +a^2 cos^2 ψ+b^2 sin^2 ψ −2R(bsin ψ+acos ψ) ...(ii) (ds^2 /dψ)=(b^2 −a^2 )sin 2ψ−2R(bcos ψ−asin ψ) (ds^2 /dψ)=0 ⇒ (b^2 −a^2 )=R((b/(sin ψ))−(a/(cos ψ))) ...(iii) from (i),(ii), (iii)with tan ψ=m R^2 (1+m^2 )=a^2 +b^2 m^2 −2R(bm+a)(√(1+m^2 )) ...(I) and (b^2 −a^2 )m=R(b−a)(√(1+m^2 )) ⇒ (b+a)m=R(√(1+m^2 )) (a≠b) ⇒ (m/( (√(1+m^2 ))))=(R/(b+a)) And (1/(1+m^2 ))=(((b+a)^2 −R^2 )/((b+a)^2 )) substituting for R(m) in (I) (b+a)^2 m^2 =a^2 +b^2 m^2 −2m(b+a)(bm+a) ⇒ a^2 m^2 +2abm^2 = a^2 −2b^2 m^2 −2abm−2abm^2 −2a^2 m (a^2 +4ab+2b^2 )m^2 +2a(a+b)m−a^2 =0 m=((−a(a+b))/((a+b)^2 +2b(a+b))) +(√((a^2 (a+b)^2 +a^2 (a+b)^2 +2a^2 b(a+b))/([(a+b)^2 +2b(a+b)]^2 ))) now (m/( (√(1+m^2 ))))=(R/(b+a)) ⇒ R=((m(a+b))/( (√(1+m^2 ))))

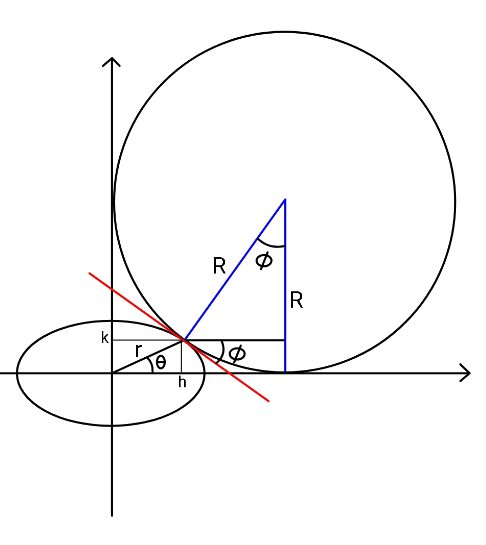
$${A}\:{Point}\:{of}\:{ellipse}\:\left({a}\mathrm{cos}\:\psi,{b}\mathrm{sin}\:\psi\right) \\ $$$${let}\:{s}\:{is}\:{distance}\:{of}\:{this}\:{point}\:\: \\ $$$${from}\:{center}\:{of}\:{circle}. \\ $$$${s}^{\mathrm{2}} =\left({R}−{a}\mathrm{cos}\:\psi\right)^{\mathrm{2}} +\left({R}−{b}\mathrm{sin}\:\psi\right)^{\mathrm{2}} \\ $$$${s}_{{min}} ={R}\:\:\:\:...\left({i}\right) \\ $$$${s}^{\mathrm{2}} =\mathrm{2}{R}^{\mathrm{2}} +{a}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \psi+{b}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \psi \\ $$$$\:\:\:\:\:\:\:−\mathrm{2}{R}\left({b}\mathrm{sin}\:\psi+{a}\mathrm{cos}\:\psi\right)\:\:...\left({ii}\right) \\ $$$$\frac{{ds}^{\mathrm{2}} }{{d}\psi}=\left({b}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)\mathrm{sin}\:\mathrm{2}\psi−\mathrm{2}{R}\left({b}\mathrm{cos}\:\psi−{a}\mathrm{sin}\:\psi\right) \\ $$$$\frac{{ds}^{\mathrm{2}} }{{d}\psi}=\mathrm{0}\:\:\:\Rightarrow \\ $$$$\left({b}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)={R}\left(\frac{{b}}{\mathrm{sin}\:\psi}−\frac{{a}}{\mathrm{cos}\:\psi}\right)\:\:...\left({iii}\right) \\ $$$${from}\:\left({i}\right),\left({ii}\right),\:\left({iii}\right){with}\:\mathrm{tan}\:\psi={m} \\ $$$${R}^{\mathrm{2}} \left(\mathrm{1}+{m}^{\mathrm{2}} \right)={a}^{\mathrm{2}} +{b}^{\mathrm{2}} {m}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:−\mathrm{2}{R}\left({bm}+{a}\right)\sqrt{\mathrm{1}+{m}^{\mathrm{2}} }\:\:...\left({I}\right) \\ $$$${and}\:\:\left({b}^{\mathrm{2}} −{a}^{\mathrm{2}} \right){m}={R}\left({b}−{a}\right)\sqrt{\mathrm{1}+{m}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\:\left({b}+{a}\right){m}={R}\sqrt{\mathrm{1}+{m}^{\mathrm{2}} }\:\:\left({a}\neq{b}\right) \\ $$$$\Rightarrow\:\:\frac{{m}}{\:\sqrt{\mathrm{1}+{m}^{\mathrm{2}} }}=\frac{{R}}{{b}+{a}} \\ $$$${And}\:\:\:\:\frac{\mathrm{1}}{\mathrm{1}+{m}^{\mathrm{2}} }=\frac{\left({b}+{a}\right)^{\mathrm{2}} −{R}^{\mathrm{2}} }{\left({b}+{a}\right)^{\mathrm{2}} } \\ $$$${substituting}\:{for}\:{R}\left({m}\right)\:{in}\:\left({I}\right) \\ $$$$\:\left({b}+{a}\right)^{\mathrm{2}} {m}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} {m}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{2}{m}\left({b}+{a}\right)\left({bm}+{a}\right) \\ $$$$\Rightarrow\:{a}^{\mathrm{2}} {m}^{\mathrm{2}} +\mathrm{2}{abm}^{\mathrm{2}} \\ $$$$\:\:\:=\:{a}^{\mathrm{2}} −\mathrm{2}{b}^{\mathrm{2}} {m}^{\mathrm{2}} −\mathrm{2}{abm}−\mathrm{2}{abm}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:−\mathrm{2}{a}^{\mathrm{2}} {m} \\ $$$$\left({a}^{\mathrm{2}} +\mathrm{4}{ab}+\mathrm{2}{b}^{\mathrm{2}} \right){m}^{\mathrm{2}} +\mathrm{2}{a}\left({a}+{b}\right){m}−{a}^{\mathrm{2}} =\mathrm{0} \\ $$$${m}=\frac{−{a}\left({a}+{b}\right)}{\left({a}+{b}\right)^{\mathrm{2}} +\mathrm{2}{b}\left({a}+{b}\right)} \\ $$$$\:+\sqrt{\frac{{a}^{\mathrm{2}} \left({a}+{b}\right)^{\mathrm{2}} +{a}^{\mathrm{2}} \left({a}+{b}\right)^{\mathrm{2}} +\mathrm{2}{a}^{\mathrm{2}} {b}\left({a}+{b}\right)}{\left[\left({a}+{b}\right)^{\mathrm{2}} +\mathrm{2}{b}\left({a}+{b}\right)\right]^{\mathrm{2}} }} \\ $$$${now}\:\:\frac{{m}}{\:\sqrt{\mathrm{1}+{m}^{\mathrm{2}} }}=\frac{{R}}{{b}+{a}} \\ $$$$\Rightarrow\:\:{R}=\frac{{m}\left({a}+{b}\right)}{\:\sqrt{\mathrm{1}+{m}^{\mathrm{2}} }}\:\: \\ $$

Commented by PRITHWISH SEN 2 last updated on 28/Dec/20

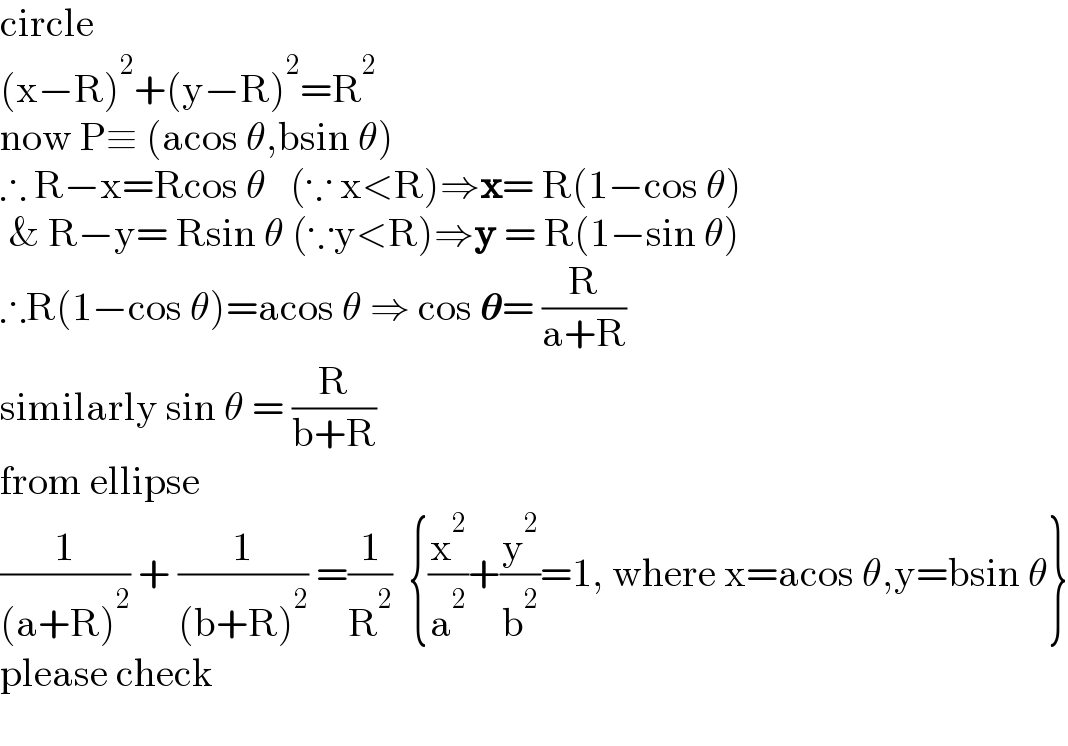
circle (x−R)^2 +(y−R)^2 =R^2 now P≡ (acos θ,bsin θ) ∴ R−x=Rcos θ (∵ x<R)⇒x= R(1−cos θ) & R−y= Rsin θ (∵y<R)⇒y = R(1−sin θ) ∴R(1−cos θ)=acos θ ⇒ cos 𝛉= (R/(a+R)) similarly sin θ = (R/(b+R)) from ellipse (1/((a+R)^2 )) + (1/((b+R)^2 )) =(1/R^2 ) {(x^2 /a^2 )+(y^2 /b^2 )=1, where x=acos θ,y=bsin θ} please check

$$\mathrm{circle} \\ $$$$\left(\mathrm{x}−\mathrm{R}\right)^{\mathrm{2}} +\left(\mathrm{y}−\mathrm{R}\right)^{\mathrm{2}} =\mathrm{R}^{\mathrm{2}} \\ $$$$\mathrm{now}\:\mathrm{P}\equiv\:\left(\mathrm{acos}\:\theta,\mathrm{bsin}\:\theta\right) \\ $$$$\therefore\:\mathrm{R}−\mathrm{x}=\mathrm{Rcos}\:\theta\:\:\:\left(\because\:\mathrm{x}<\mathrm{R}\right)\Rightarrow\boldsymbol{\mathrm{x}}=\:\mathrm{R}\left(\mathrm{1}−\mathrm{cos}\:\theta\right) \\ $$$$\:\&\:\mathrm{R}−\mathrm{y}=\:\mathrm{Rsin}\:\theta\:\left(\because\mathrm{y}<\mathrm{R}\right)\Rightarrow\boldsymbol{\mathrm{y}}\:=\:\mathrm{R}\left(\mathrm{1}−\mathrm{sin}\:\theta\right) \\ $$$$\therefore\mathrm{R}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)=\mathrm{acos}\:\theta\:\Rightarrow\:\mathrm{cos}\:\boldsymbol{\theta}=\:\frac{\mathrm{R}}{\mathrm{a}+\mathrm{R}} \\ $$$$\mathrm{similarly}\:\mathrm{sin}\:\theta\:=\:\frac{\mathrm{R}}{\mathrm{b}+\mathrm{R}} \\ $$$$\mathrm{from}\:\mathrm{ellipse} \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{a}+\mathrm{R}\right)^{\mathrm{2}} }\:+\:\frac{\mathrm{1}}{\left(\mathrm{b}+\mathrm{R}\right)^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{R}^{\mathrm{2}} }\:\:\left\{\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} }+\frac{\mathrm{y}^{\mathrm{2}} }{\mathrm{b}^{\mathrm{2}} }=\mathrm{1},\:\mathrm{where}\:\mathrm{x}=\mathrm{acos}\:\theta,\mathrm{y}=\mathrm{bsin}\:\theta\right\} \\ $$$$\mathrm{please}\:\mathrm{check} \\ $$$$ \\ $$

Commented by PRITHWISH SEN 2 last updated on 28/Dec/20

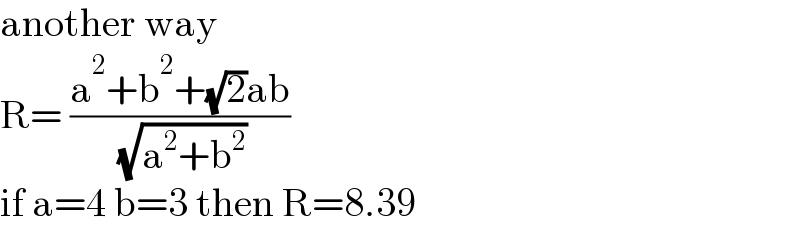
another way R= ((a^2 +b^2 +(√2)ab)/( (√(a^2 +b^2 )))) if a=4 b=3 then R=8.39

$$\mathrm{another}\:\mathrm{way} \\ $$$$\mathrm{R}=\:\frac{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\sqrt{\mathrm{2}}\mathrm{ab}}{\:\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }} \\ $$$$\mathrm{if}\:\mathrm{a}=\mathrm{4}\:\mathrm{b}=\mathrm{3}\:\mathrm{then}\:\mathrm{R}=\mathrm{8}.\mathrm{39} \\ $$

Commented by PRITHWISH SEN 2 last updated on 28/Dec/20

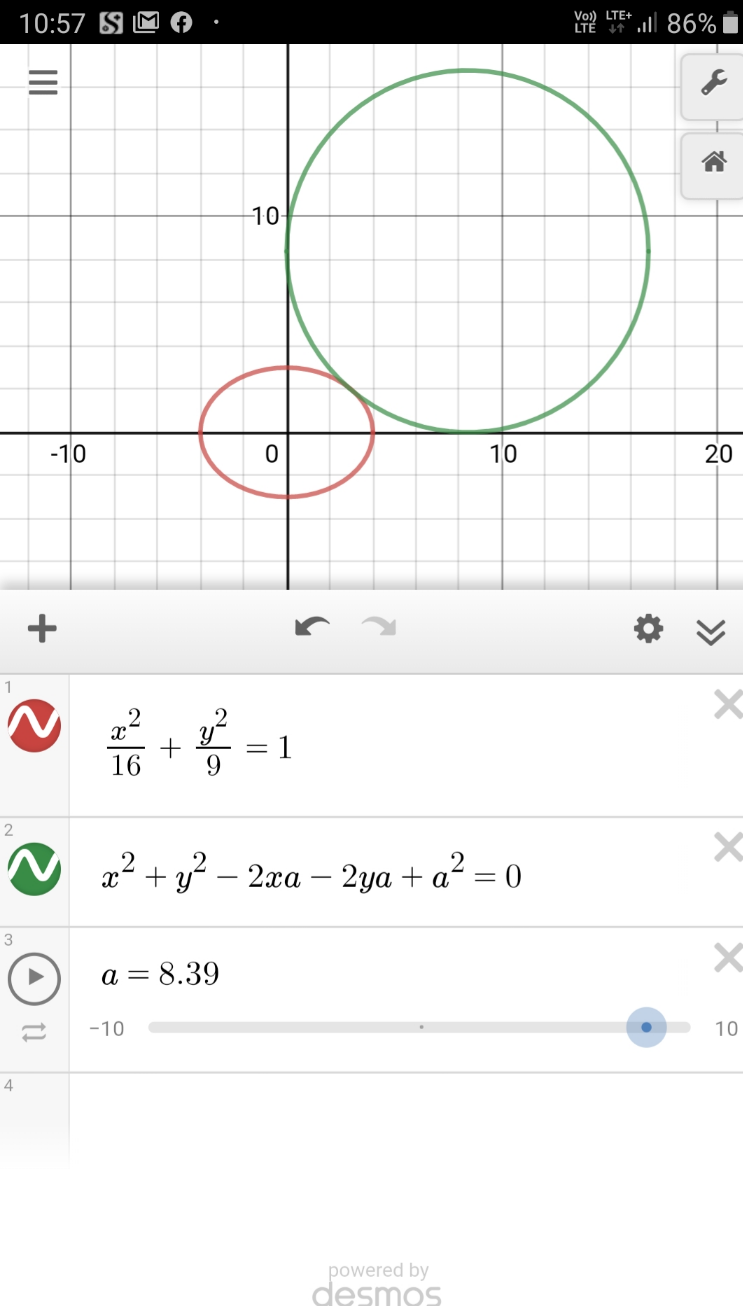
Commented by PRITHWISH SEN 2 last updated on 28/Dec/20

∵ for this particular problem there is only one P for fixed values of a & b and point P is totally depends on a & b let the point P be = ((a^2 /( (√(a^2 +b^2 )))) ,(b^2 /( (√(a^2 +b^2 ))))) putting this at (x−R)^2 +(y−R)^2 =R^2 we get R= ((a^2 +b^2 ±(√2)ab)/( (√(a^2 +b^2 )))) consider only the positive value ∵ R>a>b

$$\because\:\mathrm{for}\:\mathrm{this}\:\mathrm{particular}\:\mathrm{problem}\:\mathrm{there}\:\mathrm{is}\:\mathrm{only}\:\mathrm{one}\:\mathrm{P} \\ $$$$\mathrm{for}\:\mathrm{fixed}\:\mathrm{values}\:\mathrm{of}\:\mathrm{a}\:\&\:\mathrm{b} \\ $$$$\mathrm{and}\:\:\mathrm{point}\:\mathrm{P}\:\mathrm{is}\:\mathrm{totally}\:\mathrm{depends}\:\mathrm{on}\:\mathrm{a}\:\&\:\mathrm{b} \\ $$$$\mathrm{let}\:\mathrm{the}\:\mathrm{point}\:\mathrm{P}\:\mathrm{be}\:=\:\left(\frac{\mathrm{a}^{\mathrm{2}} }{\:\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }}\:,\frac{\mathrm{b}^{\mathrm{2}} }{\:\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }}\right) \\ $$$$\mathrm{putting}\:\mathrm{this}\:\mathrm{at} \\ $$$$\left(\mathrm{x}−\mathrm{R}\right)^{\mathrm{2}} +\left(\mathrm{y}−\mathrm{R}\right)^{\mathrm{2}} =\mathrm{R}^{\mathrm{2}} \\ $$$$\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{R}=\:\frac{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \pm\sqrt{\mathrm{2}}\mathrm{ab}}{\:\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }}\:\:\:\boldsymbol{\mathrm{consider}}\:\boldsymbol{\mathrm{only}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{positive}}\:\boldsymbol{\mathrm{value}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\because\:\boldsymbol{\mathrm{R}}>\boldsymbol{\mathrm{a}}>\boldsymbol{\mathrm{b}} \\ $$

Commented by ajfour last updated on 28/Dec/20

Great!

$${Great}! \\ $$

Commented by mr W last updated on 28/Dec/20

thanks for showing your working sir Prithwish! but this easy looking solution is in fact not correct. the error lies in following step: P≡ (acos 𝛉,bsin 𝛉) ✓ ∴ R−x≠Rcos θ (only true if ellipse is circle) & R−y≠ Rsin θ (only true if ellipse is circle) correct is: R−x=R cos ϕ R−y=R sin ϕ with ϕ ≠𝛉 (ϕ=θ only if the ellipse is a circle) you have graphed an example with a=4, b=3 which is nearly a circle, therefore the graph seems to be ok, but in fact the graph is wrong, because the big circle doesn′t tangent the ellipse really, but just intersects it. if you take an example like a=4, b=1 which is clearly not near a circle, then you′ll see that the graph is clearly not correct:

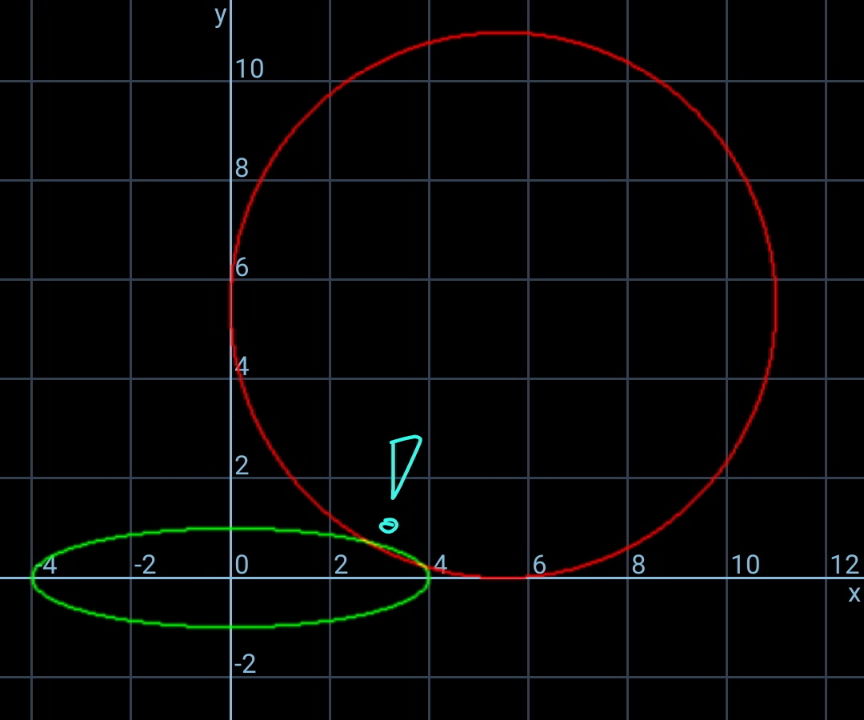
$${thanks}\:{for}\:{showing}\:{your}\:{working} \\ $$$${sir}\:{Prithwish}! \\ $$$${but}\:{this}\:{easy}\:{looking}\:{solution}\:{is}\:{in} \\ $$$${fact}\:{not}\:{correct}. \\ $$$${the}\:{error}\:{lies}\:{in}\:{following}\:{step}: \\ $$$$\mathrm{P}\equiv\:\left(\mathrm{acos}\:\boldsymbol{\theta},\mathrm{bsin}\:\boldsymbol{\theta}\right)\:\checkmark \\ $$$$\therefore\:\mathrm{R}−\mathrm{x}\neq\mathrm{Rcos}\:\theta\:\:\left({only}\:{true}\:{if}\:{ellipse}\:{is}\:{circle}\right) \\ $$$$\:\&\:\mathrm{R}−\mathrm{y}\neq\:\mathrm{Rsin}\:\theta\:\:\left({only}\:{true}\:{if}\:{ellipse}\:{is}\:{circle}\right) \\ $$$$ \\ $$$${correct}\:{is}: \\ $$$${R}−{x}={R}\:\mathrm{cos}\:\varphi \\ $$$${R}−{y}={R}\:\mathrm{sin}\:\varphi \\ $$$${with}\:\varphi\:\neq\boldsymbol{\theta} \\ $$$$\left(\varphi=\theta\:{only}\:{if}\:{the}\:{ellipse}\:{is}\:{a}\:{circle}\right) \\ $$$$ \\ $$$${you}\:{have}\:{graphed}\:{an}\:{example}\:{with} \\ $$$${a}=\mathrm{4},\:{b}=\mathrm{3}\:{which}\:{is}\:{nearly}\:{a}\:{circle}, \\ $$$${therefore}\:{the}\:{graph}\:{seems}\:{to}\:{be}\:{ok}, \\ $$$${but}\:{in}\:{fact}\:{the}\:{graph}\:{is}\:{wrong},\:{because} \\ $$$${the}\:{big}\:{circle}\:{doesn}'{t}\:{tangent}\:{the} \\ $$$${ellipse}\:{really},\:{but}\:{just}\:{intersects}\:{it}. \\ $$$$ \\ $$$${if}\:{you}\:{take}\:{an}\:{example}\:{like} \\ $$$${a}=\mathrm{4},\:{b}=\mathrm{1}\:{which}\:{is}\:{clearly}\:{not}\:{near} \\ $$$${a}\:{circle},\:{then}\:{you}'{ll}\:{see}\:{that}\:{the}\:{graph} \\ $$$${is}\:{clearly}\:{not}\:{correct}: \\ $$

Commented by mr W last updated on 28/Dec/20

Commented by ajfour last updated on 30/Dec/20

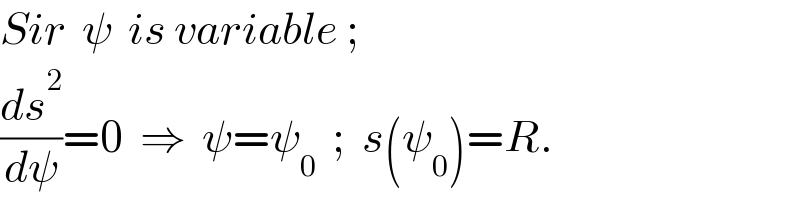
Sir ψ is variable ; (ds^2 /dψ)=0 ⇒ ψ=ψ_0 ; s(ψ_0 )=R.

$${Sir}\:\:\psi\:\:{is}\:{variable}\:; \\ $$$$\frac{{ds}^{\mathrm{2}} }{{d}\psi}=\mathrm{0}\:\:\Rightarrow\:\:\psi=\psi_{\mathrm{0}} \:\:;\:\:{s}\left(\psi_{\mathrm{0}} \right)={R}. \\ $$

Commented by ajfour last updated on 28/Dec/20

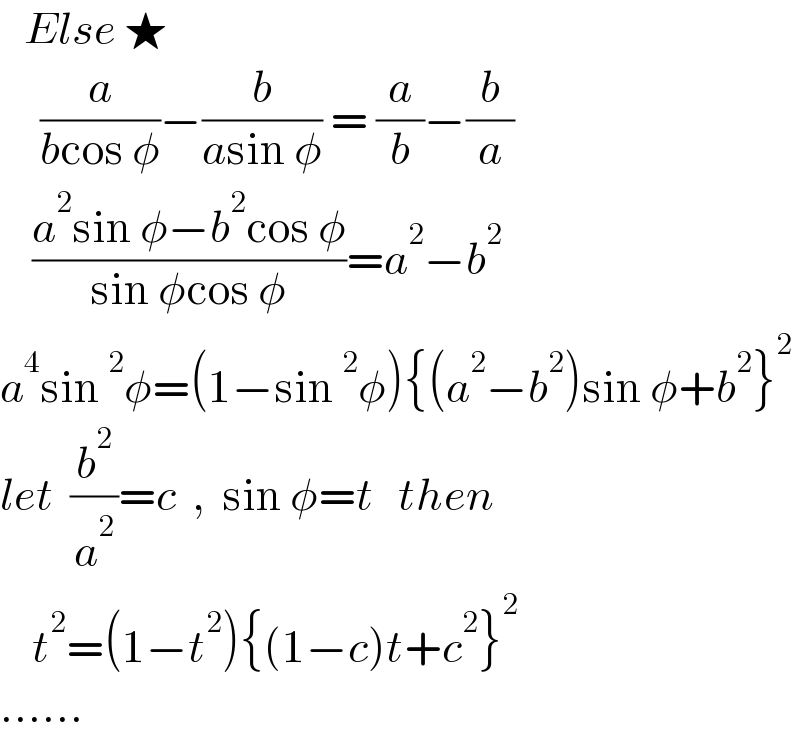
Else ★ (a/(bcos φ))−(b/(asin φ)) = (a/b)−(b/a) ((a^2 sin φ−b^2 cos φ)/(sin φcos φ))=a^2 −b^2 a^4 sin^2 φ=(1−sin^2 φ){(a^2 −b^2 )sin φ+b^2 }^2 let (b^2 /a^2 )=c , sin φ=t then t^2 =(1−t^2 ){(1−c)t+c^2 }^2 ......

$$\:\:\:{Else}\:\bigstar \\ $$$$\:\:\:\:\:\frac{{a}}{{b}\mathrm{cos}\:\phi}−\frac{{b}}{{a}\mathrm{sin}\:\phi}\:=\:\frac{{a}}{{b}}−\frac{{b}}{{a}} \\ $$$$\:\:\:\:\frac{{a}^{\mathrm{2}} \mathrm{sin}\:\phi−{b}^{\mathrm{2}} \mathrm{cos}\:\phi}{\mathrm{sin}\:\phi\mathrm{cos}\:\phi}={a}^{\mathrm{2}} −{b}^{\mathrm{2}} \\ $$$${a}^{\mathrm{4}} \mathrm{sin}\:^{\mathrm{2}} \phi=\left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \phi\right)\left\{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\mathrm{sin}\:\phi+{b}^{\mathrm{2}} \right\}^{\mathrm{2}} \\ $$$${let}\:\:\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }={c}\:\:,\:\:\mathrm{sin}\:\phi={t}\:\:\:{then} \\ $$$$\:\:\:\:{t}^{\mathrm{2}} =\left(\mathrm{1}−{t}^{\mathrm{2}} \right)\left\{\left(\mathrm{1}−{c}\right){t}+{c}^{\mathrm{2}} \right\}^{\mathrm{2}} \\ $$$$...... \\ $$

Commented by mr W last updated on 28/Dec/20

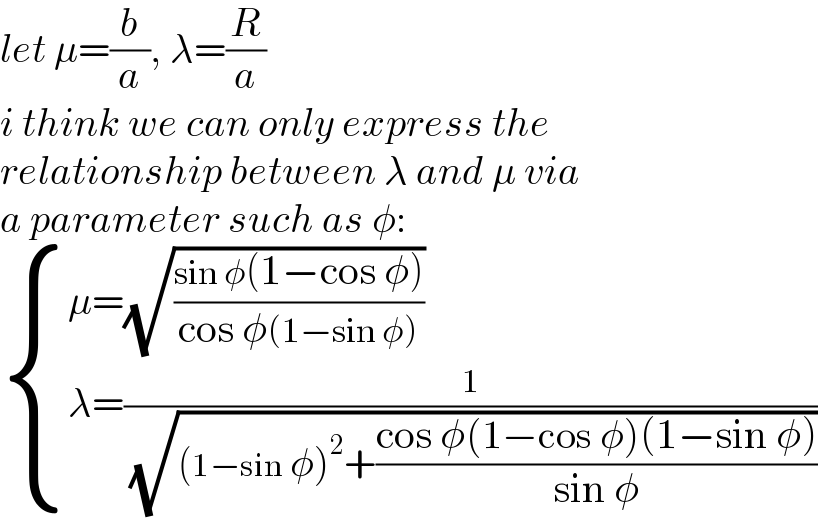
let μ=(b/a), λ=(R/a) i think we can only express the relationship between λ and μ via a parameter such as φ: { ((μ=(√((sin φ(1−cos φ))/(cos φ(1−sin φ)))))),((λ=(1/( (√((1−sin φ)^2 +((cos φ(1−cos φ)(1−sin φ))/(sin φ)))))))) :}

$${let}\:\mu=\frac{{b}}{{a}},\:\lambda=\frac{{R}}{{a}} \\ $$$${i}\:{think}\:{we}\:{can}\:{only}\:{express}\:{the} \\ $$$${relationship}\:{between}\:\lambda\:{and}\:\mu\:{via} \\ $$$${a}\:{parameter}\:{such}\:{as}\:\phi: \\ $$$$\begin{cases}{\mu=\sqrt{\frac{\mathrm{sin}\:\phi\left(\mathrm{1}−\mathrm{cos}\:\phi\right)}{\mathrm{cos}\:\phi\left(\mathrm{1}−\mathrm{sin}\:\phi\right)}}}\\{\lambda=\frac{\mathrm{1}}{\:\sqrt{\left(\mathrm{1}−\mathrm{sin}\:\phi\right)^{\mathrm{2}} +\frac{\mathrm{cos}\:\phi\left(\mathrm{1}−\mathrm{cos}\:\phi\right)\left(\mathrm{1}−\mathrm{sin}\:\phi\right)}{\mathrm{sin}\:\phi}}}}\end{cases} \\ $$

Commented by mr W last updated on 28/Dec/20

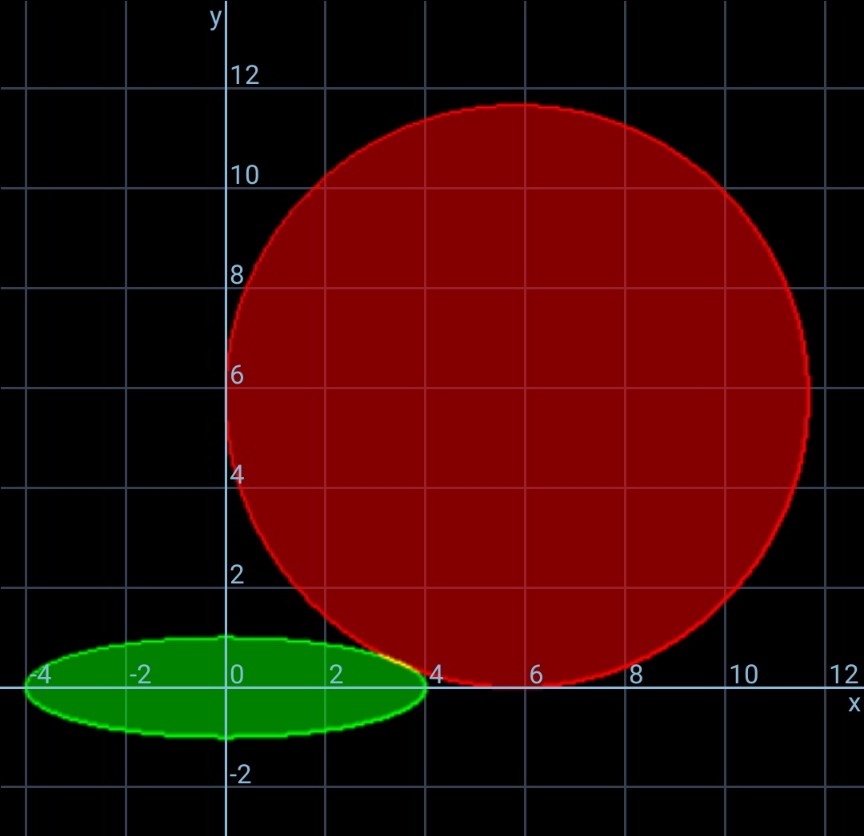
Commented by mr W last updated on 30/Dec/20

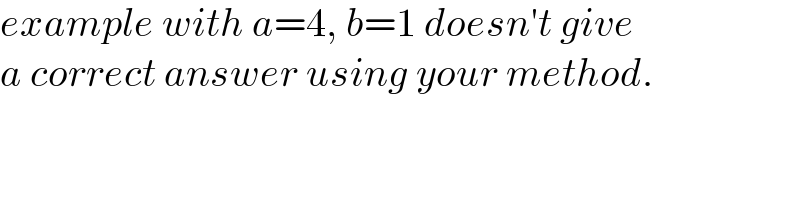
example with a=4, b=1 doesn′t give a correct answer using your method.

$${example}\:{with}\:{a}=\mathrm{4},\:{b}=\mathrm{1}\:{doesn}'{t}\:{give} \\ $$$${a}\:{correct}\:{answer}\:{using}\:{your}\:{method}. \\ $$

Commented by mr W last updated on 30/Dec/20

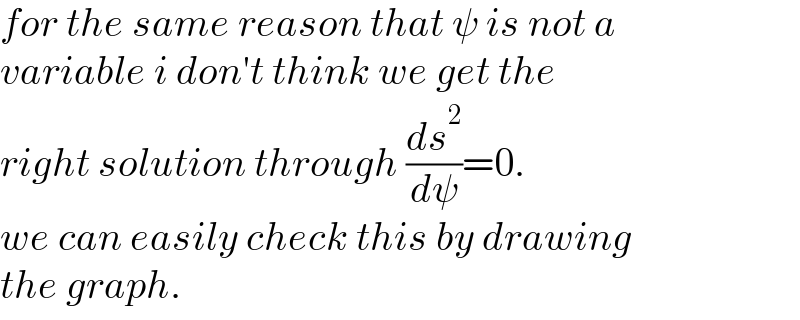
for the same reason that ψ is not a variable i don′t think we get the right solution through (ds^2 /dψ)=0. we can easily check this by drawing the graph.

$${for}\:{the}\:{same}\:{reason}\:{that}\:\psi\:{is}\:{not}\:{a} \\ $$$${variable}\:{i}\:{don}'{t}\:{think}\:{we}\:{get}\:{the}\: \\ $$$${right}\:{solution}\:{through}\:\frac{{ds}^{\mathrm{2}} }{{d}\psi}=\mathrm{0}. \\ $$$${we}\:{can}\:{easily}\:{check}\:{this}\:{by}\:{drawing} \\ $$$${the}\:{graph}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com