
Question Number 126672 by shaker last updated on 23/Dec/20
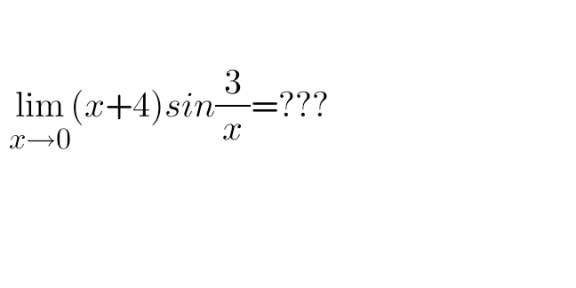
Answered by liberty last updated on 23/Dec/20
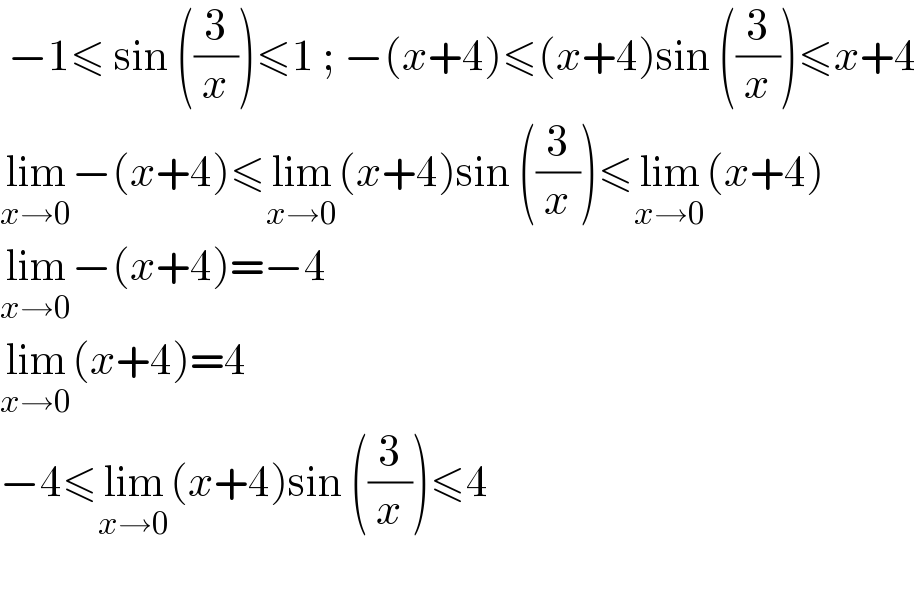
$$\:−\mathrm{1}\leqslant\:\mathrm{sin}\:\left(\frac{\mathrm{3}}{{x}}\right)\leqslant\mathrm{1}\:;\:−\left({x}+\mathrm{4}\right)\leqslant\left({x}+\mathrm{4}\right)\mathrm{sin}\:\left(\frac{\mathrm{3}}{{x}}\right)\leqslant{x}+\mathrm{4} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}−\left({x}+\mathrm{4}\right)\leqslant\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left({x}+\mathrm{4}\right)\mathrm{sin}\:\left(\frac{\mathrm{3}}{{x}}\right)\leqslant\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left({x}+\mathrm{4}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}−\left({x}+\mathrm{4}\right)=−\mathrm{4} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left({x}+\mathrm{4}\right)=\mathrm{4} \\ $$$$−\mathrm{4}\leqslant\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left({x}+\mathrm{4}\right)\mathrm{sin}\:\left(\frac{\mathrm{3}}{{x}}\right)\leqslant\mathrm{4}\: \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 24/Dec/20
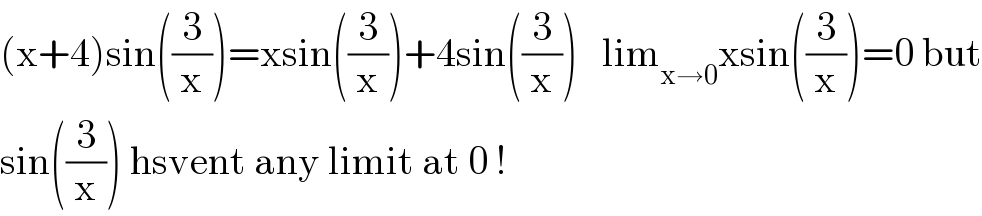
$$\left(\mathrm{x}+\mathrm{4}\right)\mathrm{sin}\left(\frac{\mathrm{3}}{\mathrm{x}}\right)=\mathrm{xsin}\left(\frac{\mathrm{3}}{\mathrm{x}}\right)+\mathrm{4sin}\left(\frac{\mathrm{3}}{\mathrm{x}}\right)\:\:\:\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \mathrm{xsin}\left(\frac{\mathrm{3}}{\mathrm{x}}\right)=\mathrm{0}\:\mathrm{but} \\ $$$$\mathrm{sin}\left(\frac{\mathrm{3}}{\mathrm{x}}\right)\:\mathrm{hsvent}\:\mathrm{any}\:\mathrm{limit}\:\mathrm{at}\:\mathrm{0}\:! \\ $$
