
Question Number 126238 by mohammad17 last updated on 18/Dec/20
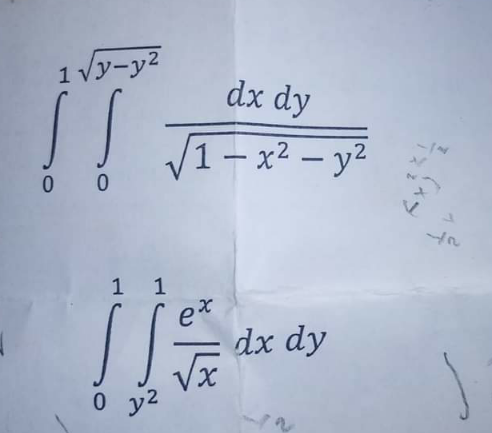
Answered by Olaf last updated on 18/Dec/20
![Ω = ∫_0 ^1 ∫_y^2 ^1 (e^x /( (√x)))dxdy Let u = (√x) Ω = ∫_0 ^1 ∫_y ^1 (e^u^2 /( u))(2udu)dy Ω = 2∫_0 ^1 ∫_y ^1 e^u^2 dudy Ω = 2∫_0 ^1 [((√π)/2)erfi(u)]_y ^1 dy Ω = (√π)∫_0 ^1 [erfi(1)−erfi(y)]dy erfi(z) = (2/( (√π)))Σ_(n=0) ^∞ (1/((2n+1)n!))z^(2n+1) Ω = 2Σ_(n=0) ^∞ (1/((2n+1)n!))∫_0 ^1 (1−y^(2n+1) )dy Ω = 2Σ_(n=0) ^∞ (1/((2n+1)n!))[y−(y^(2n+2) /(2n+2))]_0 ^1 Ω = 2Σ_(n=0) ^∞ (1/((2n+1)n!))[1−(1/(2n+2))] Ω = 2Σ_(n=0) ^∞ (1/((2n+1)n!))[((2n+1)/(2n+2))] Ω = 2Σ_(n=0) ^∞ (1/((2n+2)n!)) Ω = 2Σ_(n=0) ^∞ (1/(2(n+1)n!)) Ω = Σ_(n=0) ^∞ (1/((n+1)!)) Ω = Σ_(n=0) ^∞ (1/(n!))−1 = e−1](Q126240.png)
$$\Omega\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \int_{{y}^{\mathrm{2}} } ^{\mathrm{1}} \frac{{e}^{{x}} }{\:\sqrt{{x}}}{dxdy} \\ $$$$\mathrm{Let}\:{u}\:=\:\sqrt{{x}} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \int_{{y}} ^{\mathrm{1}} \frac{{e}^{{u}^{\mathrm{2}} } }{\:{u}}\left(\mathrm{2}{udu}\right){dy} \\ $$$$\Omega\:=\:\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \int_{{y}} ^{\mathrm{1}} {e}^{{u}^{\mathrm{2}} } {dudy} \\ $$$$\Omega\:=\:\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \left[\frac{\sqrt{\pi}}{\mathrm{2}}\mathrm{erfi}\left({u}\right)\right]_{{y}} ^{\mathrm{1}} {dy} \\ $$$$\Omega\:=\:\sqrt{\pi}\int_{\mathrm{0}} ^{\mathrm{1}} \left[\mathrm{erfi}\left(\mathrm{1}\right)−\mathrm{erfi}\left({y}\right)\right]{dy} \\ $$$$\mathrm{erfi}\left({z}\right)\:=\:\frac{\mathrm{2}}{\:\sqrt{\pi}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right){n}!}{z}^{\mathrm{2}{n}+\mathrm{1}} \\ $$$$\Omega\:=\:\mathrm{2}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right){n}!}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{y}^{\mathrm{2}{n}+\mathrm{1}} \right){dy} \\ $$$$\Omega\:=\:\mathrm{2}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right){n}!}\left[{y}−\frac{{y}^{\mathrm{2}{n}+\mathrm{2}} }{\mathrm{2}{n}+\mathrm{2}}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\Omega\:=\:\mathrm{2}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right){n}!}\left[\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{2}}\right] \\ $$$$\Omega\:=\:\mathrm{2}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right){n}!}\left[\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}{n}+\mathrm{2}}\right] \\ $$$$\Omega\:=\:\mathrm{2}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{2}\right){n}!} \\ $$$$\Omega\:=\:\mathrm{2}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}\left({n}+\mathrm{1}\right){n}!} \\ $$$$\Omega\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)!} \\ $$$$\Omega\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}−\mathrm{1}\:=\:{e}−\mathrm{1} \\ $$
Answered by Olaf last updated on 18/Dec/20
![Ω = ∫_0 ^1 ∫_0 ^(√(y−y^2 )) ((dxdy)/( (√(1−x^2 −y^2 )))) Ω = ∫_0 ^1 ∫_0 ^(√(y−y^2 )) ((dx/( (√((1−y^2 )−x^2 )))))dy ∫(dx/( (√(a^2 −x^2 )))) = arctan((x/( (√(a^2 −x^2 ))))) here a^2 = 1−y^2 Ω = ∫_0 ^1 [arctan((x/( (√((1−y^2 )−x^2 )))))]_0 ^(√(y−y^2 )) dy Ω = ∫_0 ^1 arctan(((√(y−y^2 ))/( (√((1−y^2 )−(y−y^2 ))))))dy Ω = ∫_0 ^1 arctan(((√(y−y^2 ))/( (√(1−y)))))dy Ω = ∫_0 ^1 arctan((√y))dy Let u = (√y) Ω = ∫_0 ^1 arctanu(2udu) Ω = 2∫_0 ^1 u.arctanu.du Ω = 2{[(u^2 /2)arctanu]_0 ^1 −∫_0 ^1 (u^2 /2).(du/(1+u^2 ))} Ω = (π/4)−∫_0 ^1 (u^2 /(1+u^2 ))du Ω = (π/4)−∫_0 ^1 (1−(1/(1+u^2 )))du Ω = (π/4)−[u−arctanu]_0 ^1 Ω = (π/4)−[1−(π/4)] Ω = (π/2)−1](Q126243.png)
$$\Omega\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\sqrt{{y}−{y}^{\mathrm{2}} }} \frac{{dxdy}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\sqrt{{y}−{y}^{\mathrm{2}} }} \left(\frac{{dx}}{\:\sqrt{\left(\mathrm{1}−{y}^{\mathrm{2}} \right)−{x}^{\mathrm{2}} }}\right){dy} \\ $$$$\int\frac{{dx}}{\:\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }}\:=\:\mathrm{arctan}\left(\frac{{x}}{\:\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }}\right) \\ $$$$\mathrm{here}\:{a}^{\mathrm{2}} \:=\:\mathrm{1}−{y}^{\mathrm{2}} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \left[\mathrm{arctan}\left(\frac{{x}}{\:\sqrt{\left(\mathrm{1}−{y}^{\mathrm{2}} \right)−{x}^{\mathrm{2}} }}\right)\right]_{\mathrm{0}} ^{\sqrt{{y}−{y}^{\mathrm{2}} }} {dy} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{arctan}\left(\frac{\sqrt{{y}−{y}^{\mathrm{2}} }}{\:\sqrt{\left(\mathrm{1}−{y}^{\mathrm{2}} \right)−\left({y}−{y}^{\mathrm{2}} \right)}}\right){dy} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{arctan}\left(\frac{\sqrt{{y}−{y}^{\mathrm{2}} }}{\:\sqrt{\mathrm{1}−{y}}}\right){dy} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{arctan}\left(\sqrt{{y}}\right){dy} \\ $$$$\mathrm{Let}\:{u}\:=\:\sqrt{{y}} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{arctan}{u}\left(\mathrm{2}{udu}\right) \\ $$$$\Omega\:=\:\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} {u}.\mathrm{arctan}{u}.{du} \\ $$$$\Omega\:=\:\mathrm{2}\left\{\left[\frac{{u}^{\mathrm{2}} }{\mathrm{2}}\mathrm{arctan}{u}\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{u}^{\mathrm{2}} }{\mathrm{2}}.\frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} }\right\} \\ $$$$\Omega\:=\:\frac{\pi}{\mathrm{4}}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{2}} }{du} \\ $$$$\Omega\:=\:\frac{\pi}{\mathrm{4}}−\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }\right){du} \\ $$$$\Omega\:=\:\frac{\pi}{\mathrm{4}}−\left[{u}−\mathrm{arctan}{u}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\Omega\:=\:\frac{\pi}{\mathrm{4}}−\left[\mathrm{1}−\frac{\pi}{\mathrm{4}}\right] \\ $$$$\Omega\:=\:\frac{\pi}{\mathrm{2}}−\mathrm{1} \\ $$
Answered by Ar Brandon last updated on 19/Dec/20
![I=∫_0 ^1 ∫_0 ^(√(y−y^2 )) ((dxdy)/( (√(1−x^2 −y^2 ))))=∫_0 ^1 ∫_0 ^(√(y−y^2 )) ((dxdy)/( (√((1−y^2 )−x^2 )))) =∫_0 ^1 [Arcsin((x/( (√(1−y^2 )))))]_0 ^(√(y−y^2 )) dy=∫_0 ^1 Arcsin((√((y−y^2 )/(1−y^2 ))))dy =∫_0 ^1 Arcsin((√(y/(y+1))))dy By part { ((u(y)=Arcsin((√(y/(y+1)))))),((v′(y)=1)) :}⇒ { ((u′(y)=(1/((y+1)^2 ))∙(1/2)∙(√((y+1)/y))∙(1/( (√(1−(y/(y+1)))))))),((v(y)=y)) :} ⇒ { ((u′(y)=(1/((y+1)^2 ))∙(1/2)∙(√((y+1)/y))∙(√((y+1)/1)))),((v(y)=y)) :}⇒ { ((u′(y)=(1/(2(y+1)(√y))))),((v(y)=y)) :} I={yArcsin((√(y/(y+1))))−∫(y/(2(y+1)(√y)))dy}_0 ^1 =Arcsin((1/( (√2))))−(1/2)∫_0 ^1 ((√y)/(y+1))dy Let y=t^2 ⇒ dy=2tdt I=(π/4)−(1/2)∫_0 ^1 (t/(t^2 +1))∙2tdt=(π/4)−∫_0 ^1 (t^2 /(t^2 +1))dt =(π/4)−∫_0 ^1 {1−(1/(t^2 +1))}dt=(π/4)−[t−Arctan(t)]_0 ^1 =(π/4)−1+(π/4)=(π/2)−1](Q126246.png)
$$\mathcal{I}=\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\sqrt{\mathrm{y}−\mathrm{y}^{\mathrm{2}} }} \frac{\mathrm{dxdy}}{\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} }}=\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\sqrt{\mathrm{y}−\mathrm{y}^{\mathrm{2}} }} \frac{\mathrm{dxdy}}{\:\sqrt{\left(\mathrm{1}−\mathrm{y}^{\mathrm{2}} \right)−\mathrm{x}^{\mathrm{2}} }} \\ $$$$\:\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \left[\mathrm{Arcsin}\left(\frac{\mathrm{x}}{\:\sqrt{\mathrm{1}−\mathrm{y}^{\mathrm{2}} }}\right)\right]_{\mathrm{0}} ^{\sqrt{\mathrm{y}−\mathrm{y}^{\mathrm{2}} }} \mathrm{dy}=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{Arcsin}\left(\sqrt{\frac{\mathrm{y}−\mathrm{y}^{\mathrm{2}} }{\mathrm{1}−\mathrm{y}^{\mathrm{2}} }}\right)\mathrm{dy} \\ $$$$\:\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{Arcsin}\left(\sqrt{\frac{\mathrm{y}}{\mathrm{y}+\mathrm{1}}}\right)\mathrm{dy} \\ $$$$\mathrm{By}\:\mathrm{part} \\ $$$$\begin{cases}{\mathrm{u}\left(\mathrm{y}\right)=\mathrm{Arcsin}\left(\sqrt{\frac{\mathrm{y}}{\mathrm{y}+\mathrm{1}}}\right)}\\{\mathrm{v}'\left(\mathrm{y}\right)=\mathrm{1}}\end{cases}\Rightarrow\begin{cases}{\mathrm{u}'\left(\mathrm{y}\right)=\frac{\mathrm{1}}{\left(\mathrm{y}+\mathrm{1}\right)^{\mathrm{2}} }\centerdot\frac{\mathrm{1}}{\mathrm{2}}\centerdot\sqrt{\frac{\mathrm{y}+\mathrm{1}}{\mathrm{y}}}\centerdot\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\frac{\mathrm{y}}{\mathrm{y}+\mathrm{1}}}}}\\{\mathrm{v}\left(\mathrm{y}\right)=\mathrm{y}}\end{cases} \\ $$$$\Rightarrow\begin{cases}{\mathrm{u}'\left(\mathrm{y}\right)=\frac{\mathrm{1}}{\left(\mathrm{y}+\mathrm{1}\right)^{\mathrm{2}} }\centerdot\frac{\mathrm{1}}{\mathrm{2}}\centerdot\sqrt{\frac{\mathrm{y}+\mathrm{1}}{\mathrm{y}}}\centerdot\sqrt{\frac{\mathrm{y}+\mathrm{1}}{\mathrm{1}}}}\\{\mathrm{v}\left(\mathrm{y}\right)=\mathrm{y}}\end{cases}\Rightarrow\begin{cases}{\mathrm{u}'\left(\mathrm{y}\right)=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{y}+\mathrm{1}\right)\sqrt{\mathrm{y}}}}\\{\mathrm{v}\left(\mathrm{y}\right)=\mathrm{y}}\end{cases} \\ $$$$\mathcal{I}=\left\{\mathrm{yArcsin}\left(\sqrt{\frac{\mathrm{y}}{\mathrm{y}+\mathrm{1}}}\right)−\int\frac{\mathrm{y}}{\mathrm{2}\left(\mathrm{y}+\mathrm{1}\right)\sqrt{\mathrm{y}}}\mathrm{dy}\right\}_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\:\:\:=\mathrm{Arcsin}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\sqrt{\mathrm{y}}}{\mathrm{y}+\mathrm{1}}\mathrm{dy} \\ $$$$\mathrm{Let}\:\mathrm{y}=\mathrm{t}^{\mathrm{2}} \:\Rightarrow\:\mathrm{dy}=\mathrm{2tdt} \\ $$$$\mathcal{I}=\frac{\pi}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{t}}{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}\centerdot\mathrm{2tdt}=\frac{\pi}{\mathrm{4}}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}\mathrm{dt} \\ $$$$\:\:\:=\frac{\pi}{\mathrm{4}}−\int_{\mathrm{0}} ^{\mathrm{1}} \left\{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}\right\}\mathrm{dt}=\frac{\pi}{\mathrm{4}}−\left[\mathrm{t}−\mathrm{Arctan}\left(\mathrm{t}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\:\:\:=\frac{\pi}{\mathrm{4}}−\mathrm{1}+\frac{\pi}{\mathrm{4}}=\frac{\pi}{\mathrm{2}}−\mathrm{1} \\ $$
