
Question Number 126073 by benjo_mathlover last updated on 17/Dec/20
Commented by benjo_mathlover last updated on 17/Dec/20
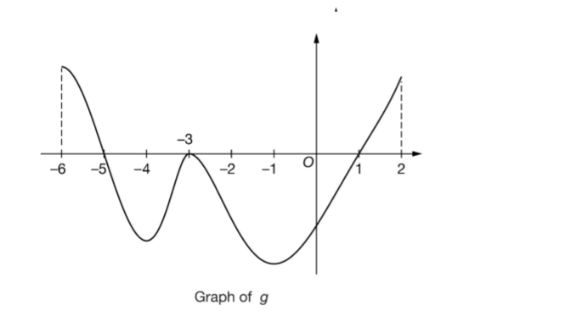
![The graph of the differentiable function g with domain −6≤x≤2 is shown in the figure above. The areas of the regions bounded by the x−axis and the graph of g on the intervals [−6,−5] [−5,−3], [ −3,1 ] and [1,2] are 9,17 42 and 6 respectively . The graph of g has horizontal tangent at x=−4 , x=−3 and x=−1. Let h be the function defined by h(x)=∫_(−3) ^( x) g(t)dt for −6≤x≤2 . Find the value of (1) h(1) (2)h(−6) (3)the x−coordinate of each critical point of h on the interval −6≤x≤2](Q126074.png)
$${The}\:{graph}\:{of}\:{the}\:{differentiable}\: \\ $$$${function}\:{g}\:{with}\:{domain}\:−\mathrm{6}\leqslant{x}\leqslant\mathrm{2}\:{is} \\ $$$${shown}\:{in}\:{the}\:{figure}\:{above}.\:{The}\:{areas} \\ $$$${of}\:{the}\:{regions}\:{bounded}\:{by}\:{the}\:{x}−{axis} \\ $$$${and}\:{the}\:{graph}\:{of}\:{g}\:{on}\:{the}\:{intervals}\:\left[−\mathrm{6},−\mathrm{5}\right] \\ $$$$\left[−\mathrm{5},−\mathrm{3}\right],\:\left[\:−\mathrm{3},\mathrm{1}\:\right]\:{and}\:\left[\mathrm{1},\mathrm{2}\right]\:{are}\:\mathrm{9},\mathrm{17} \\ $$$$\mathrm{42}\:{and}\:\mathrm{6}\:{respectively}\:.\:{The}\:{graph}\:{of}\:{g}\: \\ $$$${has}\:{horizontal}\:{tangent}\:{at}\:{x}=−\mathrm{4}\:, \\ $$$${x}=−\mathrm{3}\:{and}\:{x}=−\mathrm{1}.\:{Let}\:{h}\:{be}\:{the} \\ $$$${function}\:{defined}\:{by}\:{h}\left({x}\right)=\int_{−\mathrm{3}} ^{\:{x}} {g}\left({t}\right){dt} \\ $$$${for}\:−\mathrm{6}\leqslant{x}\leqslant\mathrm{2}\:.\:{Find}\:{the}\:{value}\:{of} \\ $$$$\left(\mathrm{1}\right)\:{h}\left(\mathrm{1}\right) \\ $$$$\left(\mathrm{2}\right){h}\left(−\mathrm{6}\right) \\ $$$$\left(\mathrm{3}\right){the}\:{x}−{coordinate}\:{of}\:{each}\:{critical} \\ $$$${point}\:{of}\:{h}\:{on}\:{the}\:{interval}\:−\mathrm{6}\leqslant{x}\leqslant\mathrm{2} \\ $$
Commented by liberty last updated on 17/Dec/20
![(1) h(1) = ∫_(−3) ^( 1) g(t) dt ; since g(t)≤0 on the interval −3≤t≤1 ; so h(1)=−[ area of the region bounded by the x−axis on [−3,1 ] h(1)=−42. (2) h(−6)= ∫_(−3) ^( −6) g(t) dt = −∫_(−6) ^(−3) g(t)dt h(−6)=−[ ∫_(−6) ^(−5) g(t)dt+∫_(−5) ^(−3) g(t)dt ] = −[ 9+(−17)] = 8](Q126075.png)
$$\left(\mathrm{1}\right)\:{h}\left(\mathrm{1}\right)\:=\:\int_{−\mathrm{3}} ^{\:\mathrm{1}} {g}\left({t}\right)\:{dt}\:;\:{since}\:{g}\left({t}\right)\leqslant\mathrm{0}\:{on}\:{the} \\ $$$${interval}\:−\mathrm{3}\leqslant{t}\leqslant\mathrm{1}\:;\:{so}\:{h}\left(\mathrm{1}\right)=−\left[\:{area}\:{of}\:{the}\:{region}\:\:\right. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{bounded}\:{by}\:{the}\:{x}−{axis}\:{on}\:\left[−\mathrm{3},\mathrm{1}\:\right] \\ $$$${h}\left(\mathrm{1}\right)=−\mathrm{42}.\: \\ $$$$\left(\mathrm{2}\right)\:{h}\left(−\mathrm{6}\right)=\:\int_{−\mathrm{3}} ^{\:−\mathrm{6}} {g}\left({t}\right)\:{dt}\:=\:−\int_{−\mathrm{6}} ^{−\mathrm{3}} {g}\left({t}\right){dt} \\ $$$$\:\:\:\:\:\:\:{h}\left(−\mathrm{6}\right)=−\left[\:\int_{−\mathrm{6}} ^{−\mathrm{5}} {g}\left({t}\right){dt}+\int_{−\mathrm{5}} ^{−\mathrm{3}} {g}\left({t}\right){dt}\:\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:−\left[\:\mathrm{9}+\left(−\mathrm{17}\right)\right]\:=\:\mathrm{8}\: \\ $$
