
Question Number 126056 by TITA last updated on 16/Dec/20

Commented by TITA last updated on 16/Dec/20

$$\mathrm{please}\:\mathrm{help} \\ $$
Answered by Olaf last updated on 16/Dec/20

$$\frac{{x}^{{x}} −\mathrm{1}}{\mathrm{ln}\left({x}+\mathrm{1}\right)}\:=\:\frac{{e}^{{x}\mathrm{ln}{x}} −\mathrm{1}}{\mathrm{ln}\left({x}+\mathrm{1}\right)} \\ $$$$\mathrm{La}\:\mathrm{limite}\:\mathrm{en}\:\mathrm{0}^{+} \:\mathrm{est}\:\mathrm{de}\:\mathrm{la}\:\mathrm{forme}\:\frac{\mathrm{0}^{+} }{\mathrm{0}^{+} }. \\ $$$$\mathrm{C}'\mathrm{est}\:\mathrm{une}\:\mathrm{forme}\:\mathrm{indeterminee}. \\ $$$$\mathrm{On}\:\mathrm{utilise}\:\mathrm{la}\:\mathrm{regle}\:\mathrm{de}\:\mathrm{l}'\mathrm{hopital}\:: \\ $$$$\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{{f}\left({x}\right)}{{g}\left({x}\right)}\:=\:\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{{f}'\left({x}\right)}{{g}'\left({x}\right)} \\ $$$$\mathrm{donc}\:\mathrm{on}\:\mathrm{cherche}\:: \\ $$$$\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\frac{\left(\mathrm{1}.\mathrm{ln}{x}+{x}.\frac{\mathrm{1}}{{x}}\right){e}^{{x}\mathrm{ln}{x}} }{\mathrm{1}/\left({x}+\mathrm{1}\right)} \\ $$$$\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\left({x}+\mathrm{1}\right)\left(\mathrm{ln}{x}+\mathrm{1}\right){e}^{{x}\mathrm{ln}{x}} \\ $$$$\mathrm{de}\:\mathrm{la}\:\mathrm{forme}\:\mathrm{1}×\left(−\infty\right)×\mathrm{1}\:\mathrm{donc}\:−\infty \\ $$
Answered by Dwaipayan Shikari last updated on 16/Dec/20
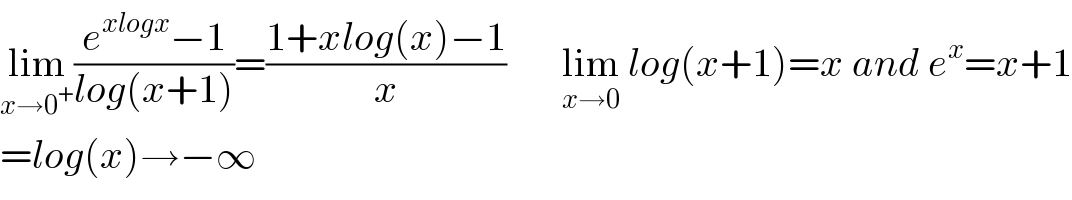
$$\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{{e}^{{xlogx}} −\mathrm{1}}{{log}\left({x}+\mathrm{1}\right)}=\frac{\mathrm{1}+{xlog}\left({x}\right)−\mathrm{1}}{{x}}\:\:\:\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{log}\left({x}+\mathrm{1}\right)={x}\:{and}\:{e}^{{x}} ={x}+\mathrm{1} \\ $$$$={log}\left({x}\right)\rightarrow−\infty \\ $$
Answered by 676597498 last updated on 17/Dec/20
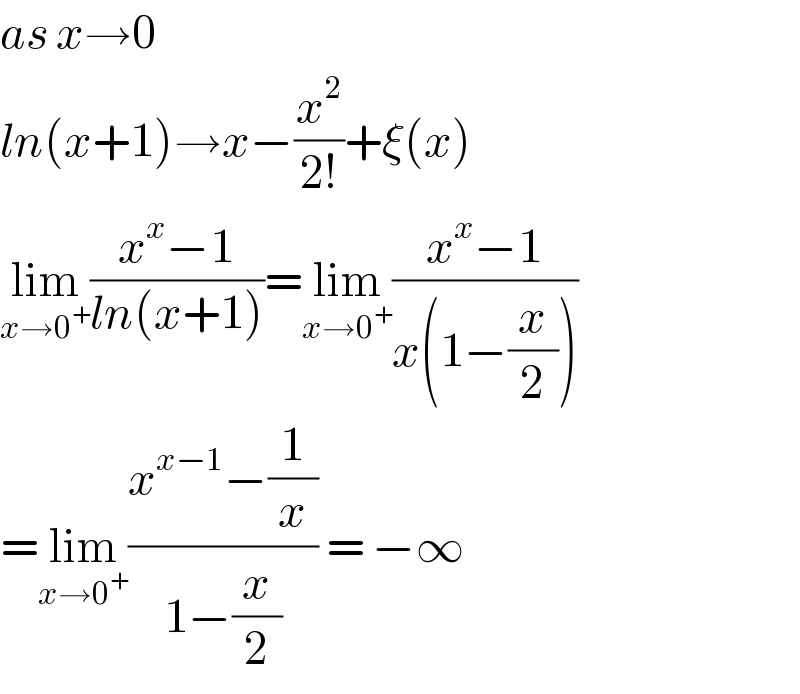
$${as}\:{x}\rightarrow\mathrm{0} \\ $$$${ln}\left({x}+\mathrm{1}\right)\rightarrow{x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\xi\left({x}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{{x}^{{x}} −\mathrm{1}}{{ln}\left({x}+\mathrm{1}\right)}=\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{{x}^{{x}} −\mathrm{1}}{{x}\left(\mathrm{1}−\frac{{x}}{\mathrm{2}}\right)} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{{x}^{{x}−\mathrm{1}} −\frac{\mathrm{1}}{{x}}}{\mathrm{1}−\frac{{x}}{\mathrm{2}}}\:=\:−\infty \\ $$
