
Question Number 125995 by liberty last updated on 16/Dec/20
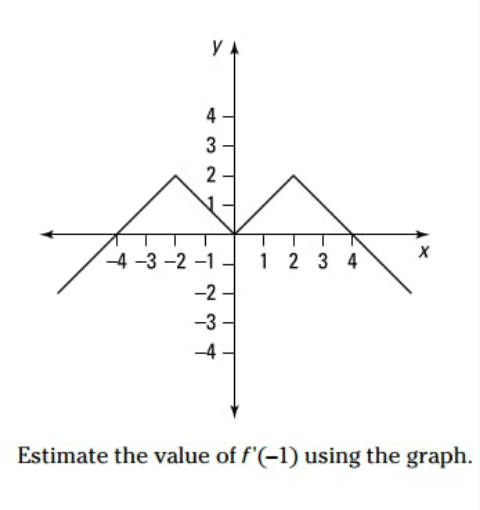
Commented by benjo_mathlover last updated on 16/Dec/20
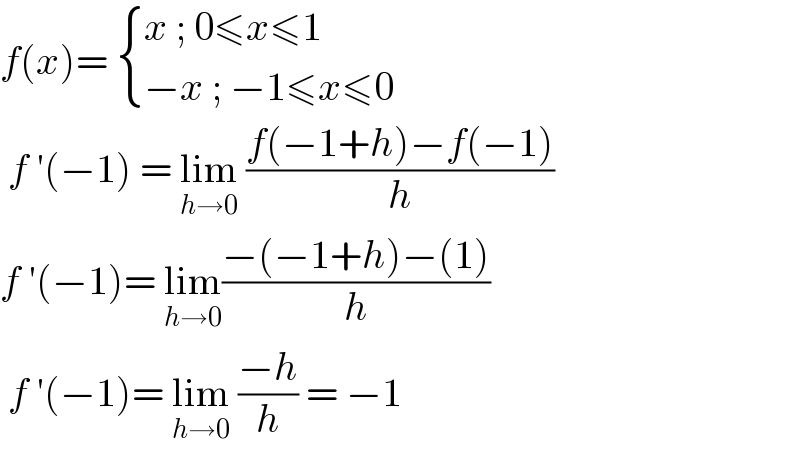
$${f}\left({x}\right)=\:\begin{cases}{{x}\:;\:\mathrm{0}\leqslant{x}\leqslant\mathrm{1}}\\{−{x}\:;\:−\mathrm{1}\leqslant{x}\leqslant\mathrm{0}}\end{cases} \\ $$$$\:{f}\:'\left(−\mathrm{1}\right)\:=\:\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{f}\left(−\mathrm{1}+{h}\right)−{f}\left(−\mathrm{1}\right)}{{h}} \\ $$$${f}\:'\left(−\mathrm{1}\right)=\:\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\left(−\mathrm{1}+{h}\right)−\left(\mathrm{1}\right)}{{h}} \\ $$$$\:{f}\:'\left(−\mathrm{1}\right)=\:\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−{h}}{{h}}\:=\:−\mathrm{1} \\ $$
