
Question Number 125028 by ngahcedric last updated on 07/Dec/20

Answered by Dwaipayan Shikari last updated on 07/Dec/20
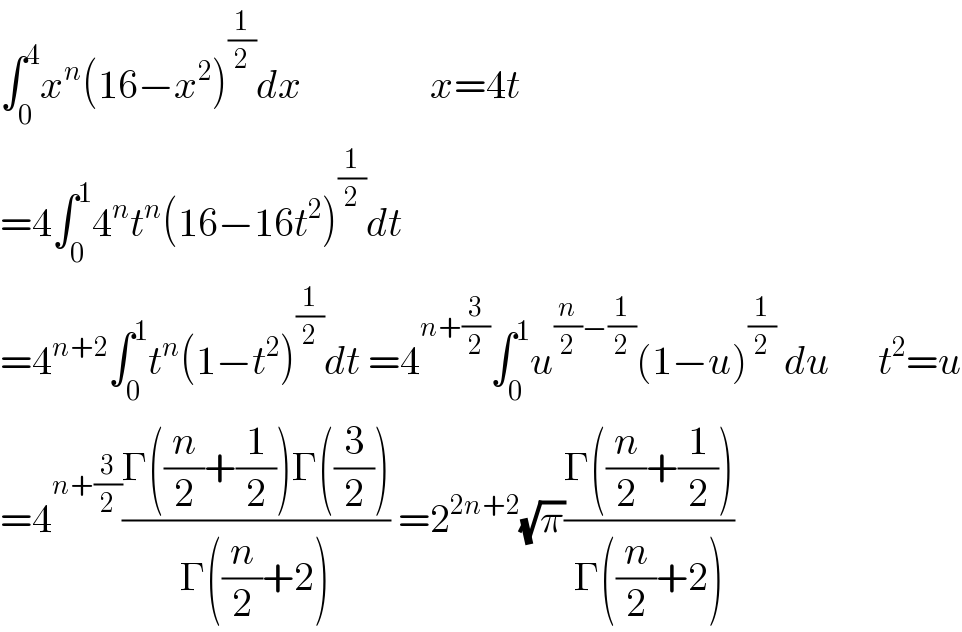
$$\int_{\mathrm{0}} ^{\mathrm{4}} {x}^{{n}} \left(\mathrm{16}−{x}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} {dx}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}=\mathrm{4}{t} \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{4}^{{n}} {t}^{{n}} \left(\mathrm{16}−\mathrm{16}{t}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} {dt} \\ $$$$=\mathrm{4}^{{n}+\mathrm{2}} \int_{\mathrm{0}} ^{\mathrm{1}} {t}^{{n}} \left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} {dt}\:=\mathrm{4}^{{n}+\frac{\mathrm{3}}{\mathrm{2}}} \int_{\mathrm{0}} ^{\mathrm{1}} {u}^{\frac{{n}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{1}−{u}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:{du}\:\:\:\:\:\:{t}^{\mathrm{2}} ={u} \\ $$$$=\mathrm{4}^{{n}+\frac{\mathrm{3}}{\mathrm{2}}} \frac{\Gamma\left(\frac{{n}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\Gamma\left(\frac{{n}}{\mathrm{2}}+\mathrm{2}\right)}\:=\mathrm{2}^{\mathrm{2}{n}+\mathrm{2}} \sqrt{\pi}\frac{\Gamma\left(\frac{{n}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left(\frac{{n}}{\mathrm{2}}+\mathrm{2}\right)} \\ $$
Commented by ngahcedric last updated on 07/Dec/20

$${don}'{t}\:{really}\:{understand} \\ $$$${please}\:{read}\:{the}\:{question}\:{well}\:{again} \\ $$
Answered by mathmax by abdo last updated on 07/Dec/20

$$\mathrm{I}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{4}\:} \mathrm{x}^{\mathrm{n}} \sqrt{\mathrm{16}−\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{x}=\mathrm{4sint}\:\Rightarrow \\ $$$$\mathrm{I}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{4}^{\mathrm{n}} \:\mathrm{sin}^{\mathrm{n}} \mathrm{t}\left(\mathrm{4cost}\right)\mathrm{4cost}\:\mathrm{dt}\:=\mathrm{4}^{\mathrm{n}+\mathrm{2}} \:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{sin}^{\mathrm{n}} \mathrm{t}\:\mathrm{cos}^{\mathrm{2}} \mathrm{t}\:\mathrm{dt} \\ $$$$\mathrm{we}\:\mathrm{hsve}\:\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{sin}^{\mathrm{2p}−\mathrm{1}} \mathrm{t}\:\mathrm{cos}^{\mathrm{2q}−\mathrm{1}} \mathrm{t}\:\mathrm{dt}\:=\mathrm{B}\left(\mathrm{p},\mathrm{q}\right)=\frac{\Gamma\left(\mathrm{p}\right).\Gamma\left(\mathrm{q}\right)}{\Gamma\left(\mathrm{p}+\mathrm{q}\right)} \\ $$$$\mathrm{2p}−\mathrm{1}=\mathrm{n}\:\Rightarrow\mathrm{p}=\frac{\mathrm{n}+\mathrm{1}}{\mathrm{2}}\:\:\mathrm{and}\:\mathrm{2q}−\mathrm{1}=\mathrm{2}\:\Rightarrow\mathrm{q}=\frac{\mathrm{3}}{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{I}_{\mathrm{n}} =\frac{\mathrm{4}^{\mathrm{n}+\mathrm{2}} }{\mathrm{2}}\mathrm{B}\left(\frac{\mathrm{n}+\mathrm{1}}{\mathrm{2}},\frac{\mathrm{3}}{\mathrm{2}}\right)\:=\frac{\mathrm{4}^{\mathrm{n}+\mathrm{2}} }{\mathrm{2}}×\frac{\Gamma\left(\frac{\mathrm{n}+\mathrm{1}}{\mathrm{2}}\right).\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\Gamma\left(\frac{\mathrm{n}+\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{2}}\right)} \\ $$$$=\mathrm{8}.\mathrm{4}^{\mathrm{n}} \:×\frac{\Gamma\left(\frac{\mathrm{n}+\mathrm{1}}{\mathrm{2}}\right)×\frac{\mathrm{1}}{\mathrm{2}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left(\frac{\mathrm{n}+\mathrm{4}}{\mathrm{2}}\right)}\:=\mathrm{4}^{\mathrm{n}+\mathrm{1}} \Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)×\frac{\Gamma\left(\frac{\mathrm{n}+\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left(\frac{\mathrm{n}+\mathrm{4}}{\mathrm{2}}\right)} \\ $$$$\mathrm{rest}\:\mathrm{to}\:\mathrm{prove}\:\mathrm{that}\:\:\frac{\mathrm{I}_{\mathrm{n}} }{\mathrm{I}_{\mathrm{n}−\mathrm{2}} }=\mathrm{16}×\frac{\mathrm{n}−\mathrm{1}}{\mathrm{n}+\mathrm{2}} \\ $$$$...\mathrm{be}\:\mathrm{continued}... \\ $$
