
Question Number 125015 by Khalmohmmad last updated on 07/Dec/20
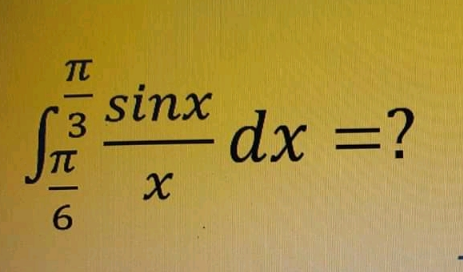
Answered by Dwaipayan Shikari last updated on 07/Dec/20
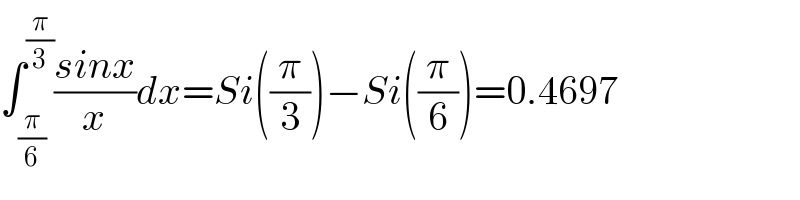
$$\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{3}}} \frac{{sinx}}{{x}}{dx}={Si}\left(\frac{\pi}{\mathrm{3}}\right)−{Si}\left(\frac{\pi}{\mathrm{6}}\right)=\mathrm{0}.\mathrm{4697} \\ $$
Answered by mathmax by abdo last updated on 07/Dec/20
![I =∫_(π/6) ^(π/3) ((sinx)/x)dx let determine spproximste vslue of I we hsve x−(x^3 /6)≤sinx≤x ⇒1−(x^2 /6)≤((sinx)/x)≤1 ⇒ ∫_(π/6) ^(π/3) (1−(x^2 /6))dx ≤∫_(π/6) ^(π/3) ((sinx)/x)dx≤(π/3)−(π/6)(=(π/6)) but ∫_(π/6) ^(π/3) (1−(x^2 /6))dx =[x−(1/(18))x^3 ]_(π/6) ^(π/3) =(π/3)−(1/(18))×(π^3 /(27))−(π/6)+(1/(18))×(π^3 /6^3 ) =(π/6)−(π^3 /(18.27))+(π^3 /(18.216)) ⇒(π/6)+((1/(18.216))−(1/(18.27)))π^3 ≤I≤(π/6) so v_0 =(π/6)+((1/(36.216))−(1/(36.27)))π^3 is a approximate value of this integral0](Q125032.png)
$$\mathrm{I}\:=\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{3}}} \:\frac{\mathrm{sinx}}{\mathrm{x}}\mathrm{dx}\:\:\mathrm{let}\:\mathrm{determine}\:\mathrm{spproximste}\:\mathrm{vslue}\:\mathrm{of}\:\mathrm{I} \\ $$$$\mathrm{we}\:\mathrm{hsve}\:\:\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}\leqslant\mathrm{sinx}\leqslant\mathrm{x}\:\Rightarrow\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{6}}\leqslant\frac{\mathrm{sinx}}{\mathrm{x}}\leqslant\mathrm{1}\:\:\Rightarrow \\ $$$$\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{3}}} \left(\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{6}}\right)\mathrm{dx}\:\leqslant\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{3}}} \:\frac{\mathrm{sinx}}{\mathrm{x}}\mathrm{dx}\leqslant\frac{\pi}{\mathrm{3}}−\frac{\pi}{\mathrm{6}}\left(=\frac{\pi}{\mathrm{6}}\right)\:\:\mathrm{but} \\ $$$$\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{3}}} \left(\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{6}}\right)\mathrm{dx}\:=\left[\mathrm{x}−\frac{\mathrm{1}}{\mathrm{18}}\mathrm{x}^{\mathrm{3}} \right]_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{3}}} =\frac{\pi}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{18}}×\frac{\pi^{\mathrm{3}} }{\mathrm{27}}−\frac{\pi}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{18}}×\frac{\pi^{\mathrm{3}} }{\mathrm{6}^{\mathrm{3}} } \\ $$$$=\frac{\pi}{\mathrm{6}}−\frac{\pi^{\mathrm{3}} }{\mathrm{18}.\mathrm{27}}+\frac{\pi^{\mathrm{3}} }{\mathrm{18}.\mathrm{216}}\:\Rightarrow\frac{\pi}{\mathrm{6}}+\left(\frac{\mathrm{1}}{\mathrm{18}.\mathrm{216}}−\frac{\mathrm{1}}{\mathrm{18}.\mathrm{27}}\right)\pi^{\mathrm{3}} \leqslant\mathrm{I}\leqslant\frac{\pi}{\mathrm{6}} \\ $$$$ \\ $$$$\mathrm{so}\:\mathrm{v}_{\mathrm{0}} =\frac{\pi}{\mathrm{6}}+\left(\frac{\mathrm{1}}{\mathrm{36}.\mathrm{216}}−\frac{\mathrm{1}}{\mathrm{36}.\mathrm{27}}\right)\pi^{\mathrm{3}} \:\:\mathrm{is}\:\mathrm{a}\:\mathrm{approximate}\:\mathrm{value}\:\mathrm{of}\:\mathrm{this} \\ $$$$\mathrm{integral0} \\ $$$$ \\ $$
