
Question Number 124988 by bemath last updated on 07/Dec/20
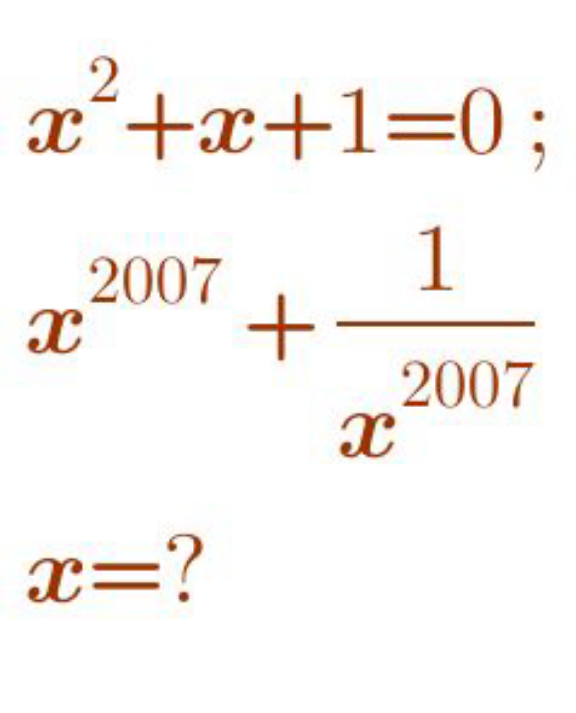
Commented by bemath last updated on 07/Dec/20

$${x}\:=\:\frac{−\mathrm{1}\pm\sqrt{\mathrm{1}−\mathrm{4}}}{\mathrm{2}}\:=\:\frac{−\mathrm{1}\pm{i}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${x}_{\mathrm{1}} \:=\:−\frac{\mathrm{1}}{\mathrm{2}}+\frac{{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:\Rightarrow{x}_{\mathrm{1}} =\:\mathrm{cos}\:\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)+\:{i}\mathrm{sin}\:\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right) \\ $$$${x}_{\mathrm{1}} ^{\mathrm{2007}} \:=\:\mathrm{cos}\:\left(\frac{\mathrm{4014}\pi}{\mathrm{3}}\right)+{i}\mathrm{sin}\:\left(\frac{\mathrm{4014}\pi}{\mathrm{3}}\right) \\ $$$${x}_{\mathrm{1}} ^{−\mathrm{2007}} \:=\:\mathrm{cos}\:\left(\frac{\mathrm{4014}\pi}{\mathrm{3}}\right)−{i}\mathrm{sin}\:\left(\frac{\mathrm{4014}\pi}{\mathrm{3}}\right) \\ $$$${x}^{\mathrm{2007}} +\frac{\mathrm{1}}{{x}^{\mathrm{2007}} }\:=\:\mathrm{2cos}\:\left(\frac{\mathrm{4014}\pi}{\mathrm{3}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{2cos}\:\left(\mathrm{1338}\pi\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{2cos}\:\left(\mathrm{0}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{2}×\left(\mathrm{1}\right)=\mathrm{2} \\ $$
Commented by floor(10²Eta[1]) last updated on 07/Dec/20
$$\mathrm{desnecessary}\:\mathrm{long}\:\mathrm{result} \\ $$
Commented by bemath last updated on 08/Dec/20
$${i}\:{like}\:{a}\:{long}\:{thing}\: \\ $$
Answered by floor(10²Eta[1]) last updated on 07/Dec/20
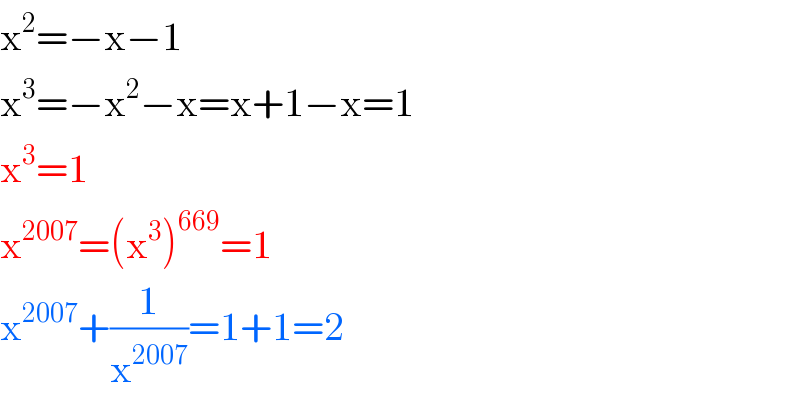
$$\mathrm{x}^{\mathrm{2}} =−\mathrm{x}−\mathrm{1} \\ $$$$\mathrm{x}^{\mathrm{3}} =−\mathrm{x}^{\mathrm{2}} −\mathrm{x}=\mathrm{x}+\mathrm{1}−\mathrm{x}=\mathrm{1} \\ $$$$\mathrm{x}^{\mathrm{3}} =\mathrm{1} \\ $$$$\mathrm{x}^{\mathrm{2007}} =\left(\mathrm{x}^{\mathrm{3}} \right)^{\mathrm{669}} =\mathrm{1} \\ $$$$\mathrm{x}^{\mathrm{2007}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2007}} }=\mathrm{1}+\mathrm{1}=\mathrm{2} \\ $$
Commented by talminator2856791 last updated on 07/Dec/20
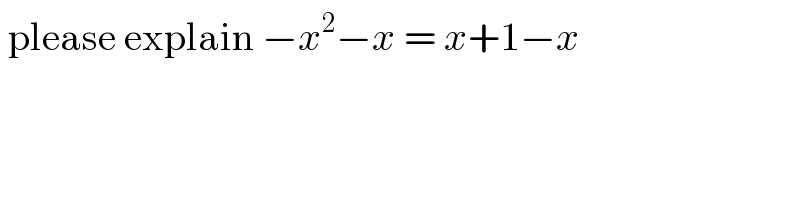
$$\:\mathrm{please}\:\mathrm{explain}\:−{x}^{\mathrm{2}} −{x}\:=\:{x}+\mathrm{1}−{x} \\ $$
Commented by floor(10²Eta[1]) last updated on 07/Dec/20

$$\mathrm{x}^{\mathrm{2}} =−\mathrm{x}−\mathrm{1} \\ $$
Commented by talminator2856791 last updated on 07/Dec/20
$$\:\mathrm{ooooooooooooo}\:\mathrm{wow} \\ $$
Commented by talminator2856791 last updated on 07/Dec/20
$$\:\mathrm{can}\:\mathrm{you}\:\mathrm{please}\:\mathrm{look}\:\mathrm{at}\:\mathrm{my}\:\mathrm{answer}\:\mathrm{for}\:\mathrm{post}\:\mathrm{124978} \\ $$
