
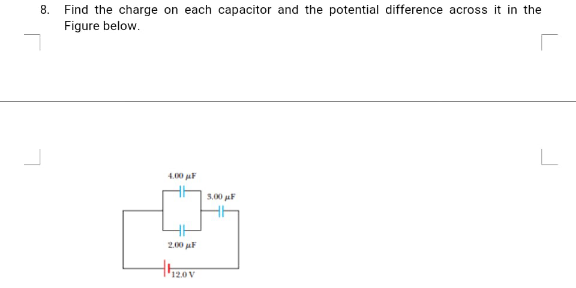
Question Number 124932 by aurpeyz last updated on 07/Dec/20
Answered by som(math1967) last updated on 07/Dec/20
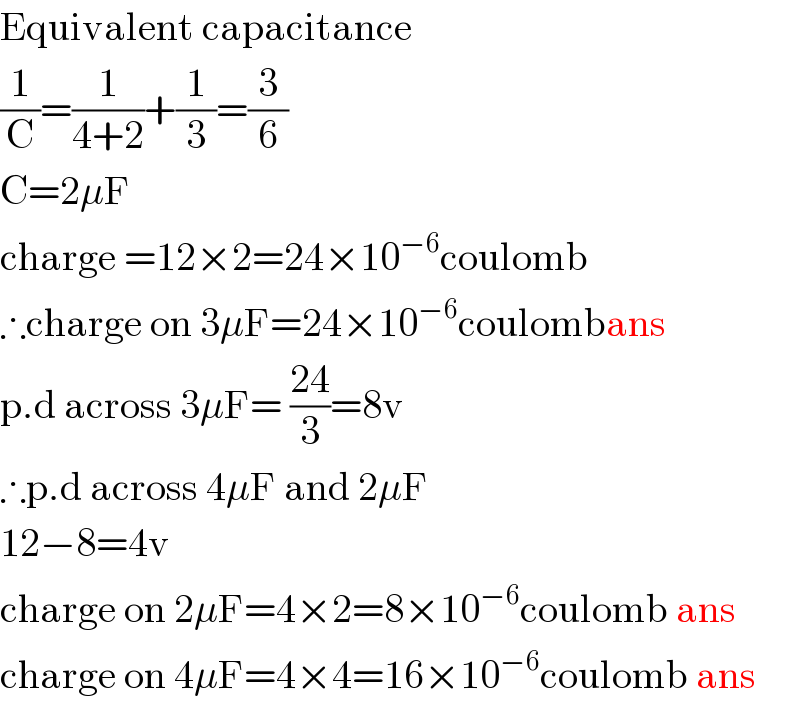
$$\mathrm{Equivalent}\:\mathrm{capacitance} \\ $$$$\frac{\mathrm{1}}{\mathrm{C}}=\frac{\mathrm{1}}{\mathrm{4}+\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{3}}{\mathrm{6}} \\ $$$$\mathrm{C}=\mathrm{2}\mu\mathrm{F} \\ $$$$\mathrm{charge}\:=\mathrm{12}×\mathrm{2}=\mathrm{24}×\mathrm{10}^{−\mathrm{6}} \mathrm{coulomb} \\ $$$$\therefore\mathrm{charge}\:\mathrm{on}\:\mathrm{3}\mu\mathrm{F}=\mathrm{24}×\mathrm{10}^{−\mathrm{6}} \mathrm{coulombans} \\ $$$$\mathrm{p}.\mathrm{d}\:\mathrm{across}\:\mathrm{3}\mu\mathrm{F}=\:\frac{\mathrm{24}}{\mathrm{3}}=\mathrm{8v} \\ $$$$\therefore\mathrm{p}.\mathrm{d}\:\mathrm{across}\:\mathrm{4}\mu\mathrm{F}\:\mathrm{and}\:\mathrm{2}\mu\mathrm{F} \\ $$$$\mathrm{12}−\mathrm{8}=\mathrm{4v} \\ $$$$\mathrm{charge}\:\mathrm{on}\:\mathrm{2}\mu\mathrm{F}=\mathrm{4}×\mathrm{2}=\mathrm{8}×\mathrm{10}^{−\mathrm{6}} \mathrm{coulomb}\:\mathrm{ans} \\ $$$$\mathrm{charge}\:\mathrm{on}\:\mathrm{4}\mu\mathrm{F}=\mathrm{4}×\mathrm{4}=\mathrm{16}×\mathrm{10}^{−\mathrm{6}} \mathrm{coulomb}\:\mathrm{ans} \\ $$
