
Question Number 124797 by oustmuchiya@gmail.com last updated on 06/Dec/20

Answered by benjo_mathlover last updated on 06/Dec/20
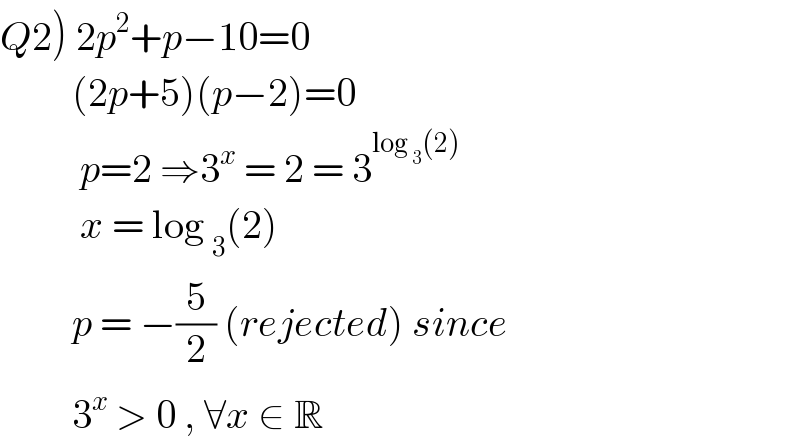
$$\left.{Q}\mathrm{2}\right)\:\mathrm{2}{p}^{\mathrm{2}} +{p}−\mathrm{10}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\left(\mathrm{2}{p}+\mathrm{5}\right)\left({p}−\mathrm{2}\right)=\mathrm{0}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:{p}=\mathrm{2}\:\Rightarrow\mathrm{3}^{{x}} \:=\:\mathrm{2}\:=\:\mathrm{3}^{\mathrm{log}\:_{\mathrm{3}} \left(\mathrm{2}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:{x}\:=\:\mathrm{log}\:_{\mathrm{3}} \left(\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:\:\:{p}\:=\:−\frac{\mathrm{5}}{\mathrm{2}}\:\left({rejected}\right)\:{since} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{3}^{{x}} \:>\:\mathrm{0}\:,\:\forall{x}\:\in\:\mathbb{R} \\ $$
Answered by benjo_mathlover last updated on 06/Dec/20
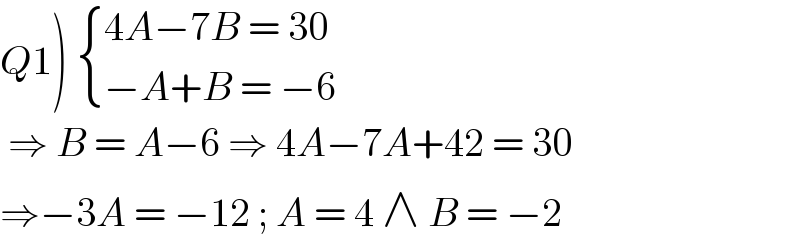
$$\left.{Q}\mathrm{1}\right)\:\begin{cases}{\mathrm{4}{A}−\mathrm{7}{B}\:=\:\mathrm{30}}\\{−{A}+{B}\:=\:−\mathrm{6}}\end{cases} \\ $$$$\:\Rightarrow\:{B}\:=\:{A}−\mathrm{6}\:\Rightarrow\:\mathrm{4}{A}−\mathrm{7}{A}+\mathrm{42}\:=\:\mathrm{30} \\ $$$$\Rightarrow−\mathrm{3}{A}\:=\:−\mathrm{12}\:;\:{A}\:=\:\mathrm{4}\:\wedge\:{B}\:=\:−\mathrm{2} \\ $$
