
Question Number 124791 by ajfour last updated on 06/Dec/20
Commented by ajfour last updated on 06/Dec/20
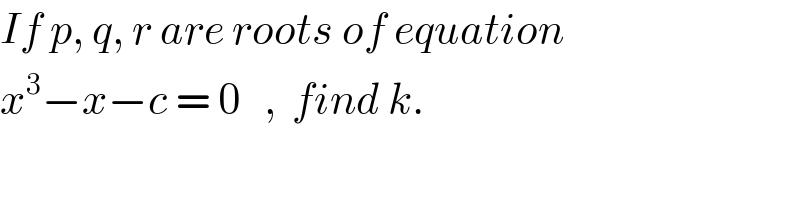
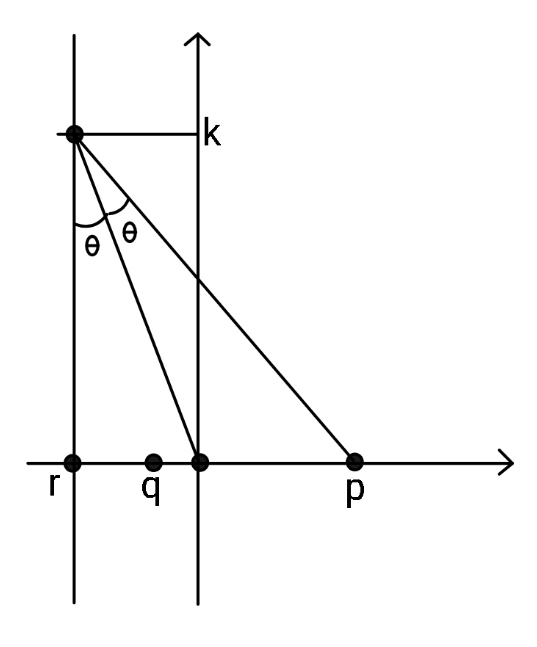
$${If}\:{p},\:{q},\:{r}\:{are}\:{roots}\:{of}\:{equation} \\ $$$${x}^{\mathrm{3}} −{x}−{c}\:=\:\mathrm{0}\:\:\:,\:\:{find}\:{k}. \\ $$
Answered by ajfour last updated on 08/Dec/20
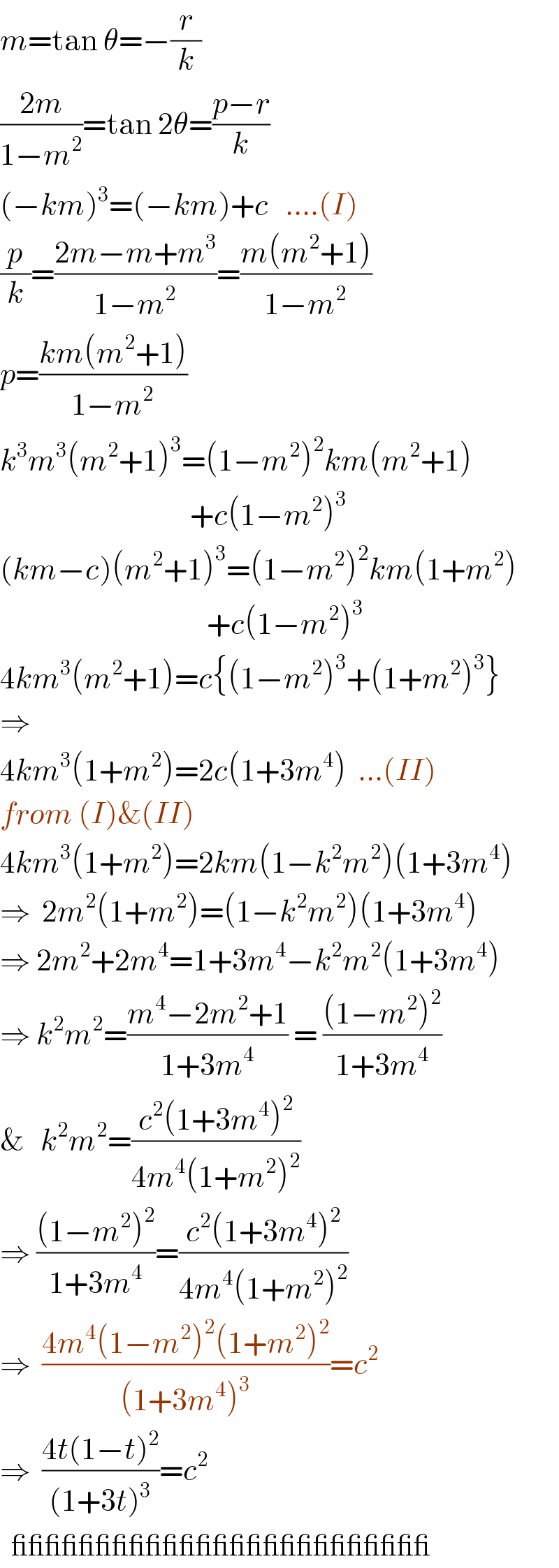
$${m}=\mathrm{tan}\:\theta=−\frac{{r}}{{k}} \\ $$$$\frac{\mathrm{2}{m}}{\mathrm{1}−{m}^{\mathrm{2}} }=\mathrm{tan}\:\mathrm{2}\theta=\frac{{p}−{r}}{{k}} \\ $$$$\left(−{km}\right)^{\mathrm{3}} =\left(−{km}\right)+{c}\:\:\:....\left({I}\right) \\ $$$$\frac{{p}}{{k}}=\frac{\mathrm{2}{m}−{m}+{m}^{\mathrm{3}} }{\mathrm{1}−{m}^{\mathrm{2}} }=\frac{{m}\left({m}^{\mathrm{2}} +\mathrm{1}\right)}{\mathrm{1}−{m}^{\mathrm{2}} } \\ $$$${p}=\frac{{km}\left({m}^{\mathrm{2}} +\mathrm{1}\right)}{\mathrm{1}−{m}^{\mathrm{2}} } \\ $$$${k}^{\mathrm{3}} {m}^{\mathrm{3}} \left({m}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} =\left(\mathrm{1}−{m}^{\mathrm{2}} \right)^{\mathrm{2}} {km}\left({m}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+{c}\left(\mathrm{1}−{m}^{\mathrm{2}} \right)^{\mathrm{3}} \\ $$$$\left({km}−{c}\right)\left({m}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} =\left(\mathrm{1}−{m}^{\mathrm{2}} \right)^{\mathrm{2}} {km}\left(\mathrm{1}+{m}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+{c}\left(\mathrm{1}−{m}^{\mathrm{2}} \right)^{\mathrm{3}} \\ $$$$\mathrm{4}{km}^{\mathrm{3}} \left({m}^{\mathrm{2}} +\mathrm{1}\right)={c}\left\{\left(\mathrm{1}−{m}^{\mathrm{2}} \right)^{\mathrm{3}} +\left(\mathrm{1}+{m}^{\mathrm{2}} \right)^{\mathrm{3}} \right\} \\ $$$$\Rightarrow \\ $$$$\mathrm{4}{km}^{\mathrm{3}} \left(\mathrm{1}+{m}^{\mathrm{2}} \right)=\mathrm{2}{c}\left(\mathrm{1}+\mathrm{3}{m}^{\mathrm{4}} \right)\:\:...\left({II}\right) \\ $$$${from}\:\left({I}\right)\&\left({II}\right) \\ $$$$\mathrm{4}{km}^{\mathrm{3}} \left(\mathrm{1}+{m}^{\mathrm{2}} \right)=\mathrm{2}{km}\left(\mathrm{1}−{k}^{\mathrm{2}} {m}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{3}{m}^{\mathrm{4}} \right) \\ $$$$\Rightarrow\:\:\mathrm{2}{m}^{\mathrm{2}} \left(\mathrm{1}+{m}^{\mathrm{2}} \right)=\left(\mathrm{1}−{k}^{\mathrm{2}} {m}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{3}{m}^{\mathrm{4}} \right) \\ $$$$\Rightarrow\:\mathrm{2}{m}^{\mathrm{2}} +\mathrm{2}{m}^{\mathrm{4}} =\mathrm{1}+\mathrm{3}{m}^{\mathrm{4}} −{k}^{\mathrm{2}} {m}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{3}{m}^{\mathrm{4}} \right) \\ $$$$\Rightarrow\:{k}^{\mathrm{2}} {m}^{\mathrm{2}} =\frac{{m}^{\mathrm{4}} −\mathrm{2}{m}^{\mathrm{2}} +\mathrm{1}}{\mathrm{1}+\mathrm{3}{m}^{\mathrm{4}} }\:=\:\frac{\left(\mathrm{1}−{m}^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{1}+\mathrm{3}{m}^{\mathrm{4}} } \\ $$$$\&\:\:\:{k}^{\mathrm{2}} {m}^{\mathrm{2}} =\frac{{c}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{3}{m}^{\mathrm{4}} \right)^{\mathrm{2}} }{\mathrm{4}{m}^{\mathrm{4}} \left(\mathrm{1}+{m}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\Rightarrow\:\frac{\left(\mathrm{1}−{m}^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{1}+\mathrm{3}{m}^{\mathrm{4}} }=\frac{{c}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{3}{m}^{\mathrm{4}} \right)^{\mathrm{2}} }{\mathrm{4}{m}^{\mathrm{4}} \left(\mathrm{1}+{m}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\Rightarrow\:\:\frac{\mathrm{4}{m}^{\mathrm{4}} \left(\mathrm{1}−{m}^{\mathrm{2}} \right)^{\mathrm{2}} \left(\mathrm{1}+{m}^{\mathrm{2}} \right)^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{3}{m}^{\mathrm{4}} \right)^{\mathrm{3}} }={c}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\frac{\mathrm{4}{t}\left(\mathrm{1}−{t}\right)^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{3}{t}\right)^{\mathrm{3}} }={c}^{\mathrm{2}} \\ $$$$\:\:\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$
