
Question Number 124192 by Algoritm last updated on 01/Dec/20
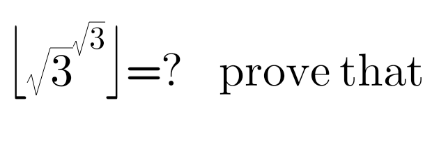
Commented by MJS_new last updated on 01/Dec/20

$$\mathrm{2} \\ $$
Commented by Algoritm last updated on 01/Dec/20

$$\mathrm{proof} \\ $$
Answered by MJS_new last updated on 01/Dec/20
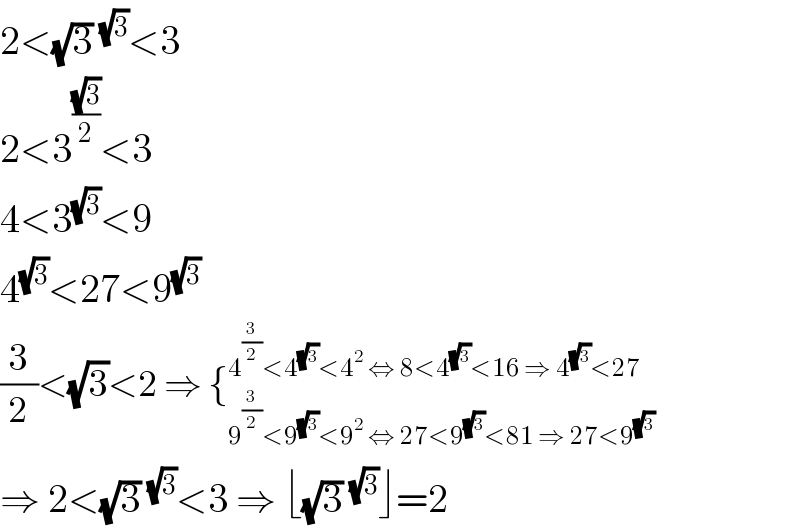
$$\mathrm{2}<\sqrt{\mathrm{3}}\:^{\sqrt{\mathrm{3}}} <\mathrm{3} \\ $$$$\mathrm{2}<\mathrm{3}^{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} <\mathrm{3} \\ $$$$\mathrm{4}<\mathrm{3}^{\sqrt{\mathrm{3}}} <\mathrm{9} \\ $$$$\mathrm{4}^{\sqrt{\mathrm{3}}} <\mathrm{27}<\mathrm{9}^{\sqrt{\mathrm{3}}} \\ $$$$\frac{\mathrm{3}}{\mathrm{2}}<\sqrt{\mathrm{3}}<\mathrm{2}\:\Rightarrow\:\left\{_{\mathrm{9}^{\frac{\mathrm{3}}{\mathrm{2}}} <\mathrm{9}^{\sqrt{\mathrm{3}}} <\mathrm{9}^{\mathrm{2}} \:\Leftrightarrow\:\mathrm{27}<\mathrm{9}^{\sqrt{\mathrm{3}}} <\mathrm{81}\:\Rightarrow\:\mathrm{27}<\mathrm{9}^{\sqrt{\mathrm{3}}} } ^{\mathrm{4}^{\frac{\mathrm{3}}{\mathrm{2}}} <\mathrm{4}^{\sqrt{\mathrm{3}}} <\mathrm{4}^{\mathrm{2}} \:\Leftrightarrow\:\mathrm{8}<\mathrm{4}^{\sqrt{\mathrm{3}}} <\mathrm{16}\:\Rightarrow\:\mathrm{4}^{\sqrt{\mathrm{3}}} <\mathrm{27}} \right. \\ $$$$\Rightarrow\:\mathrm{2}<\sqrt{\mathrm{3}}\:^{\sqrt{\mathrm{3}}} <\mathrm{3}\:\Rightarrow\:\lfloor\sqrt{\mathrm{3}}\:^{\sqrt{\mathrm{3}}} \rfloor=\mathrm{2} \\ $$
Commented by MJS_new last updated on 01/Dec/20

$$\mathrm{same}\:\mathrm{procedure} \\ $$$$\mathrm{6}<\mathrm{3}^{\sqrt{\mathrm{3}}} <\mathrm{7} \\ $$$$\mathrm{6}^{\sqrt{\mathrm{3}}} <\mathrm{27}<\mathrm{7}^{\sqrt{\mathrm{3}}} \\ $$$$\frac{\mathrm{17}}{\mathrm{10}}<\sqrt{\mathrm{3}}<\frac{\mathrm{18}}{\mathrm{10}}\:\Rightarrow\:\left\{_{\mathrm{7}^{\frac{\mathrm{17}}{\mathrm{10}}} <\mathrm{7}^{\sqrt{\mathrm{3}}} <\mathrm{7}^{\frac{\mathrm{18}}{\mathrm{10}}} } ^{\mathrm{6}^{\frac{\mathrm{17}}{\mathrm{10}}} <\mathrm{6}^{\sqrt{\mathrm{3}}} <\mathrm{6}^{\frac{\mathrm{18}}{\mathrm{10}}} } \right. \\ $$$$\mathrm{6}^{\frac{\mathrm{18}}{\mathrm{10}}} <\mathrm{27}\:\Leftrightarrow\:\mathrm{6}^{\mathrm{18}} <\mathrm{27}^{\mathrm{10}} \:\Leftrightarrow\:\mathrm{2}^{\mathrm{18}} \mathrm{3}^{\mathrm{18}} <\mathrm{3}^{\mathrm{12}} \mathrm{3}^{\mathrm{18}} \:\Leftrightarrow \\ $$$$\Leftrightarrow\:\mathrm{2}^{\mathrm{18}} <\mathrm{3}^{\mathrm{12}} \:\Leftrightarrow\:\mathrm{2}\sqrt{\mathrm{2}}<\mathrm{3}\:\mathrm{true} \\ $$$$\mathrm{27}<\mathrm{7}^{\frac{\mathrm{17}}{\mathrm{10}}} \:\Leftrightarrow\:\mathrm{27}^{\mathrm{10}} <\mathrm{7}^{\mathrm{17}} \:\Leftrightarrow\:\mathrm{205891132094649}<\mathrm{232630513987207} \\ $$$$\mathrm{true}\:\left(\mathrm{sorry}\:\mathrm{I}\:\mathrm{found}\:\mathrm{no}\:\mathrm{better}\:\mathrm{way}\right) \\ $$$$\Rightarrow\:\mathrm{6}^{\sqrt{\mathrm{3}}} <\mathrm{6}^{\frac{\mathrm{18}}{\mathrm{10}}} <\mathrm{27}<\mathrm{7}^{\frac{\mathrm{17}}{\mathrm{10}}} <\mathrm{7}^{\sqrt{\mathrm{3}}} \\ $$$$\Leftrightarrow\:\mathrm{6}<\mathrm{3}^{\sqrt{\mathrm{3}}} <\mathrm{7} \\ $$
Commented by Algoritm last updated on 01/Dec/20

$$\mathrm{Brilliant} \\ $$
Commented by Algoritm last updated on 01/Dec/20
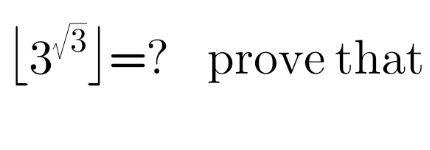
Commented by MJS_new last updated on 01/Dec/20
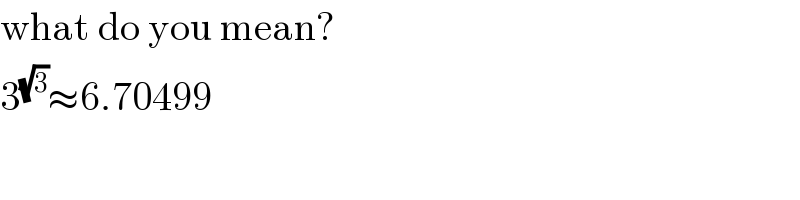
$$\mathrm{what}\:\mathrm{do}\:\mathrm{you}\:\mathrm{mean}? \\ $$$$\mathrm{3}^{\sqrt{\mathrm{3}}} \approx\mathrm{6}.\mathrm{70499} \\ $$
Commented by Algoritm last updated on 01/Dec/20

