Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 124000 by joki last updated on 30/Nov/20

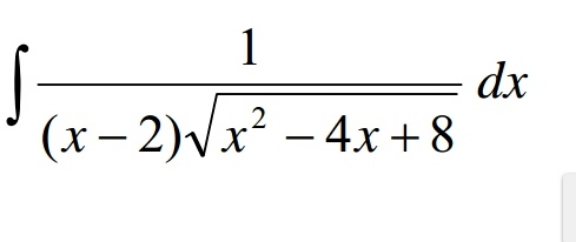
Answered by liberty last updated on 30/Nov/20

∫ (dx/((x−2)(√((x−2)^2 +2^2 )))) ;[ x−2=2tan r ] μ(x)=∫ ((2sec^2 r dr)/(2tan r (√(4sec^2 r)))) = (1/2)∫ (( dr)/(sin r)) μ(x)=(1/2)∫ cosec r dr = (1/2)ℓn ∣ cosec r − cot r ∣ + c μ(x)=ℓn (√((((√(x^2 −4x+8)) )/2)−(2/(x−2)))) + c

$$\:\int\:\frac{{dx}}{\left({x}−\mathrm{2}\right)\sqrt{\left({x}−\mathrm{2}\right)^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} }}\:\:;\left[\:{x}−\mathrm{2}=\mathrm{2tan}\:{r}\:\right] \\ $$$$\mu\left({x}\right)=\int\:\frac{\mathrm{2sec}\:^{\mathrm{2}} {r}\:{dr}}{\mathrm{2tan}\:{r}\:\sqrt{\mathrm{4sec}\:^{\mathrm{2}} {r}}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\:{dr}}{\mathrm{sin}\:{r}} \\ $$$$\mu\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\int\:\mathrm{cosec}\:{r}\:{dr}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\ell{n}\:\mid\:\mathrm{cosec}\:{r}\:−\:\mathrm{cot}\:{r}\:\mid\:+\:{c} \\ $$$$\mu\left({x}\right)=\ell{n}\:\sqrt{\frac{\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{8}}\:}{\mathrm{2}}−\frac{\mathrm{2}}{{x}−\mathrm{2}}}\:+\:{c}\: \\ $$

Answered by mathmax by abdo last updated on 30/Nov/20

A =∫ (dx/((x−2)(√(x^2 −4x+8)))) ⇒A =∫ (dx/((x−2)(√((x−2)^2 +4)))) we do the changement x−2=2sht ⇒ A =∫ ((2cht)/(2sht2cht))dt =∫ (dt/(2sh(t))) =∫ (dt/(e^t −e^(−t) )) =_(e^t =z) ∫ (dz/(z(z−z^(−1) )))=∫ (dz/(z^2 −1)) =(1/2)∫((1/(z−1))−(1/(z+1)))dz =(1/2)ln∣((z−1)/(z+1))∣ +k we have t=argsh(((x−2)/2))=ln(((x−2)/2)+(√(1+(((x−2)/2))^2 ))) ⇒z=e^t =((x−2)/2)+(√(1+(((x−2)/2))^2 )) ⇒ A =(1/2)ln∣((((x−2)/2)+((√(4+(x−2)^2 ))/2)−1∣)/(((x−2)/2)+((√(4+(x−2)^2 ))/2)+1))∣+k =(1/2)ln∣((x−4+(√((x−2)^2 +4)))/(x+(√((x−2)^2 +4))))∣ +k

$$\mathrm{A}\:=\int\:\:\frac{\mathrm{dx}}{\left(\mathrm{x}−\mathrm{2}\right)\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{8}}}\:\Rightarrow\mathrm{A}\:=\int\:\:\frac{\mathrm{dx}}{\left(\mathrm{x}−\mathrm{2}\right)\sqrt{\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} \:+\mathrm{4}}} \\ $$$$\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{x}−\mathrm{2}=\mathrm{2sht}\:\Rightarrow \\ $$$$\mathrm{A}\:=\int\:\:\:\frac{\mathrm{2cht}}{\mathrm{2sht2cht}}\mathrm{dt}\:=\int\:\:\frac{\mathrm{dt}}{\mathrm{2sh}\left(\mathrm{t}\right)}\:=\int\:\:\frac{\mathrm{dt}}{\mathrm{e}^{\mathrm{t}} −\mathrm{e}^{−\mathrm{t}} } \\ $$$$=_{\mathrm{e}^{\mathrm{t}} =\mathrm{z}} \:\:\:\int\:\:\:\frac{\mathrm{dz}}{\mathrm{z}\left(\mathrm{z}−\mathrm{z}^{−\mathrm{1}} \right)}=\int\:\frac{\mathrm{dz}}{\mathrm{z}^{\mathrm{2}} −\mathrm{1}}\:=\frac{\mathrm{1}}{\mathrm{2}}\int\left(\frac{\mathrm{1}}{\mathrm{z}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{z}+\mathrm{1}}\right)\mathrm{dz} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\frac{\mathrm{z}−\mathrm{1}}{\mathrm{z}+\mathrm{1}}\mid\:+\mathrm{k}\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{t}=\mathrm{argsh}\left(\frac{\mathrm{x}−\mathrm{2}}{\mathrm{2}}\right)=\mathrm{ln}\left(\frac{\mathrm{x}−\mathrm{2}}{\mathrm{2}}+\sqrt{\mathrm{1}+\left(\frac{\mathrm{x}−\mathrm{2}}{\mathrm{2}}\right)^{\mathrm{2}} }\right) \\ $$$$\Rightarrow\mathrm{z}=\mathrm{e}^{\mathrm{t}} \:=\frac{\mathrm{x}−\mathrm{2}}{\mathrm{2}}+\sqrt{\mathrm{1}+\left(\frac{\mathrm{x}−\mathrm{2}}{\mathrm{2}}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{A}\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\frac{\frac{\mathrm{x}−\mathrm{2}}{\mathrm{2}}+\frac{\sqrt{\mathrm{4}+\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} }}{\mathrm{2}}−\mathrm{1}\mid}{\frac{\mathrm{x}−\mathrm{2}}{\mathrm{2}}+\frac{\sqrt{\mathrm{4}+\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} }}{\mathrm{2}}+\mathrm{1}}\mid+\mathrm{k} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\frac{\mathrm{x}−\mathrm{4}+\sqrt{\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} +\mathrm{4}}}{\mathrm{x}+\sqrt{\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} +\mathrm{4}}}\mid\:+\mathrm{k} \\ $$

Answered by Ar Brandon last updated on 30/Nov/20

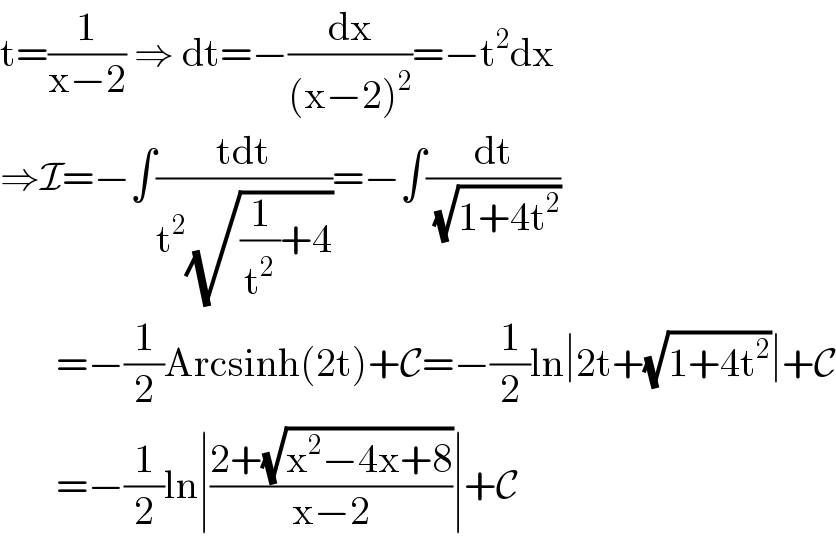
t=(1/(x−2)) ⇒ dt=−(dx/((x−2)^2 ))=−t^2 dx ⇒I=−∫((tdt)/(t^2 (√((1/t^2 )+4))))=−∫(dt/( (√(1+4t^2 )))) =−(1/2)Arcsinh(2t)+C=−(1/2)ln∣2t+(√(1+4t^2 ))∣+C =−(1/2)ln∣((2+(√(x^2 −4x+8)))/(x−2))∣+C

$$\mathrm{t}=\frac{\mathrm{1}}{\mathrm{x}−\mathrm{2}}\:\Rightarrow\:\mathrm{dt}=−\frac{\mathrm{dx}}{\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} }=−\mathrm{t}^{\mathrm{2}} \mathrm{dx} \\ $$$$\Rightarrow\mathcal{I}=−\int\frac{\mathrm{tdt}}{\mathrm{t}^{\mathrm{2}} \sqrt{\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }+\mathrm{4}}}=−\int\frac{\mathrm{dt}}{\:\sqrt{\mathrm{1}+\mathrm{4t}^{\mathrm{2}} }} \\ $$$$\:\:\:\:\:\:\:=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Arcsinh}\left(\mathrm{2t}\right)+\mathcal{C}=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\mathrm{2t}+\sqrt{\mathrm{1}+\mathrm{4t}^{\mathrm{2}} }\mid+\mathcal{C} \\ $$$$\:\:\:\:\:\:\:=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\frac{\mathrm{2}+\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{8}}}{\mathrm{x}−\mathrm{2}}\mid+\mathcal{C} \\ $$

Commented by liberty last updated on 30/Nov/20

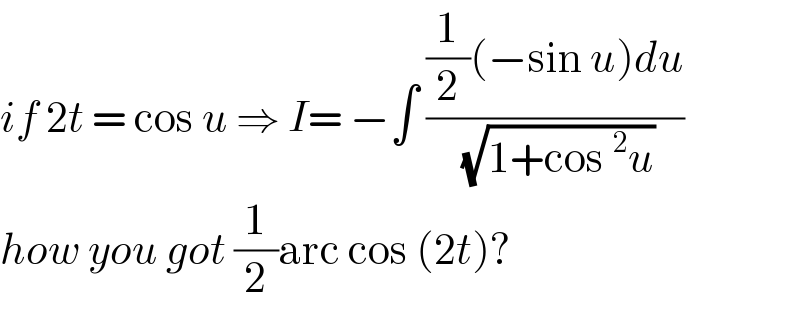
if 2t = cos u ⇒ I= −∫ (((1/2)(−sin u)du)/( (√(1+cos^2 u)))) how you got (1/2)arc cos (2t)?

$${if}\:\mathrm{2}{t}\:=\:\mathrm{cos}\:{u}\:\Rightarrow\:{I}=\:−\int\:\frac{\frac{\mathrm{1}}{\mathrm{2}}\left(−\mathrm{sin}\:{u}\right){du}}{\:\sqrt{\mathrm{1}+\mathrm{cos}\:^{\mathrm{2}} {u}}} \\ $$$${how}\:{you}\:{got}\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{arc}\:\mathrm{cos}\:\left(\mathrm{2}{t}\right)? \\ $$

Commented by Ar Brandon last updated on 30/Nov/20

Found my mistake, thanks

Answered by MJS_new last updated on 30/Nov/20

∫(dx/((x−2)(√(x^2 −4x+8))))= [t=((2+(√(x^2 −4x+8)))/(x−2)) → dx=(−(x^2 /2)+2x−4+(√(x^2 −4x+8)))dt] =−(1/2)∫(dt/t)=−(1/2)ln t = =−(1/2)ln ∣((2+(√(x^2 −4x+8)))/(x−2))∣ +C

$$\int\frac{{dx}}{\left({x}−\mathrm{2}\right)\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{8}}}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{\mathrm{2}+\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{8}}}{{x}−\mathrm{2}}\:\rightarrow\:{dx}=\left(−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{2}{x}−\mathrm{4}+\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{8}}\right){dt}\right] \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dt}}{{t}}=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:{t}\:= \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid\frac{\mathrm{2}+\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{8}}}{{x}−\mathrm{2}}\mid\:+{C} \\ $$

Answered by Dwaipayan Shikari last updated on 30/Nov/20

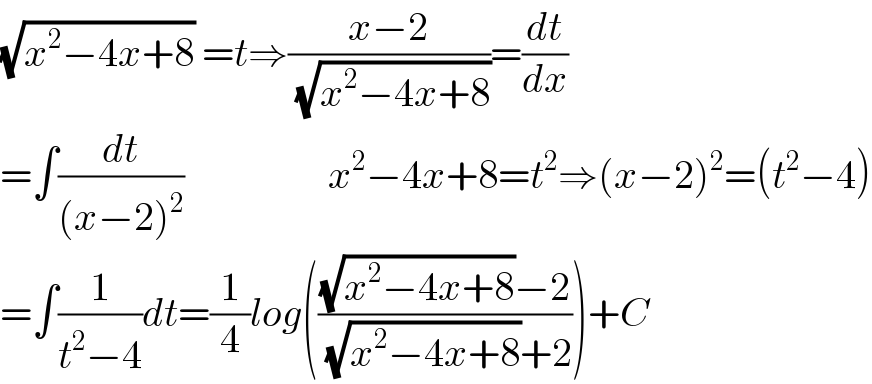
(√(x^2 −4x+8)) =t⇒((x−2)/( (√(x^2 −4x+8))))=(dt/dx) =∫(dt/((x−2)^2 )) x^2 −4x+8=t^2 ⇒(x−2)^2 =(t^2 −4) =∫(1/(t^2 −4))dt=(1/4)log((((√(x^2 −4x+8))−2)/( (√(x^2 −4x+8))+2)))+C

$$\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{8}}\:={t}\Rightarrow\frac{{x}−\mathrm{2}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{8}}}=\frac{{dt}}{{dx}} \\ $$$$=\int\frac{{dt}}{\left({x}−\mathrm{2}\right)^{\mathrm{2}} }\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{8}={t}^{\mathrm{2}} \Rightarrow\left({x}−\mathrm{2}\right)^{\mathrm{2}} =\left({t}^{\mathrm{2}} −\mathrm{4}\right) \\ $$$$=\int\frac{\mathrm{1}}{{t}^{\mathrm{2}} −\mathrm{4}}{dt}=\frac{\mathrm{1}}{\mathrm{4}}{log}\left(\frac{\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{8}}−\mathrm{2}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{8}}+\mathrm{2}}\right)+{C} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com