
Question Number 123829 by Algoritm last updated on 28/Nov/20
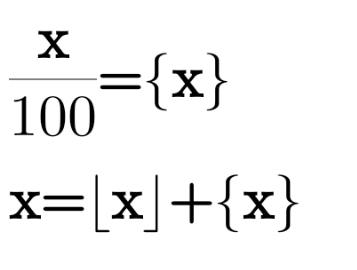
Commented by Algoritm last updated on 28/Nov/20

$$\mathrm{prove}\:\mathrm{that}\: \\ $$
Commented by mr W last updated on 28/Nov/20
![x=((100k)/(99)) with k∈[0,98]](Q123835.png)
$${x}=\frac{\mathrm{100}{k}}{\mathrm{99}}\:{with}\:{k}\in\left[\mathrm{0},\mathrm{98}\right] \\ $$
Answered by Snail last updated on 28/Nov/20
![(x/(100))=x−⌊x⌋ ⌊x⌋=((99x)/(100)) now let ⌊x⌋=m x=((100m)/(99)) where m∈[0,98] because of 0≤{x}<1](Q123853.png)
$$\frac{{x}}{\mathrm{100}}={x}−\lfloor{x}\rfloor \\ $$$$\lfloor{x}\rfloor=\frac{\mathrm{99}{x}}{\mathrm{100}} \\ $$$${now}\:{let}\:\lfloor{x}\rfloor={m} \\ $$$${x}=\frac{\mathrm{100}{m}}{\mathrm{99}} \\ $$$${where}\:{m}\in\left[\mathrm{0},\mathrm{98}\right]\:\:\:{because}\:{of}\:\mathrm{0}\leqslant\left\{{x}\right\}<\mathrm{1} \\ $$
