Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 123576 by bramlexs22 last updated on 26/Nov/20

Commented by talminator2856791 last updated on 26/Nov/20

the image is not so clear

$$\:\mathrm{the}\:\mathrm{image}\:\mathrm{is}\:\mathrm{not}\:\mathrm{so}\:\mathrm{clear} \\ $$

Commented by benjo_mathlover last updated on 26/Nov/20

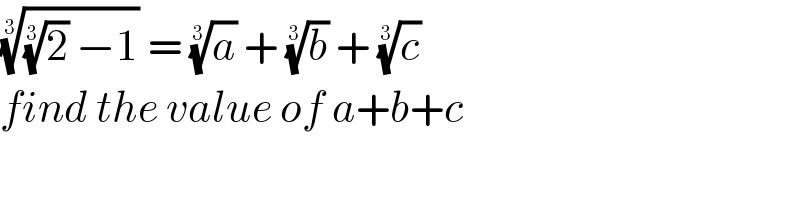
(((2)^(1/3) −1))^(1/3) = (a)^(1/3) + (b)^(1/3) + (c)^(1/3) find the value of a+b+c

$$\sqrt[{\mathrm{3}}]{\sqrt[{\mathrm{3}}]{\mathrm{2}}\:−\mathrm{1}}\:=\:\sqrt[{\mathrm{3}}]{{a}}\:+\:\sqrt[{\mathrm{3}}]{{b}}\:+\:\sqrt[{\mathrm{3}}]{{c}}\: \\ $$$${find}\:{the}\:{value}\:{of}\:{a}+{b}+{c} \\ $$

Answered by Dwaipayan Shikari last updated on 26/Nov/20

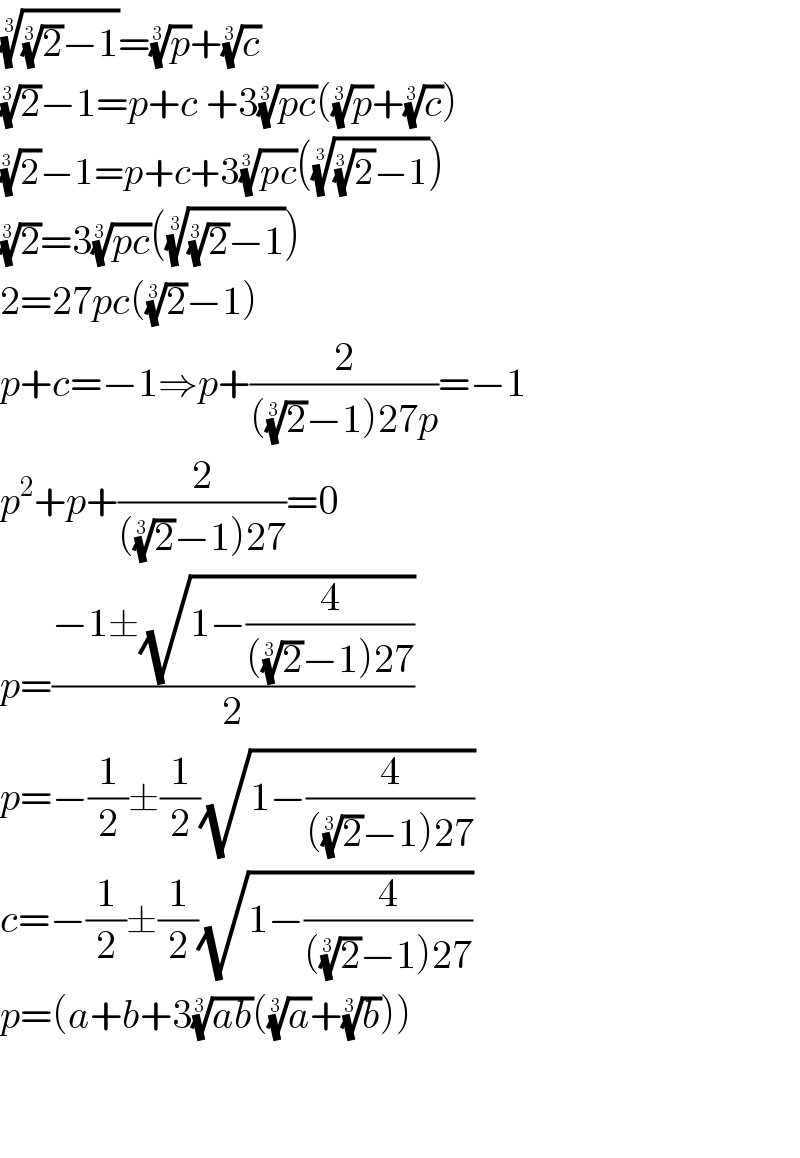
(((2)^(1/3) −1))^(1/3) =(p)^(1/3) +(c)^(1/3) (2)^(1/3) −1=p+c +3((pc))^(1/3) ((p)^(1/3) +(c)^(1/3) ) (2)^(1/3) −1=p+c+3((pc))^(1/3) ((((2)^(1/3) −1))^(1/3) ) (2)^(1/3) =3((pc))^(1/3) ((((2)^(1/3) −1))^(1/3) ) 2=27pc((2)^(1/3) −1) p+c=−1⇒p+(2/(((2)^(1/3) −1)27p))=−1 p^2 +p+(2/(((2)^(1/3) −1)27))=0 p=((−1±(√(1−(4/(((2)^(1/3) −1)27)))))/2) p=−(1/2)±(1/2)(√(1−(4/(((2)^(1/3) −1)27)))) c=−(1/2)±(1/2)(√(1−(4/(((2)^(1/3) −1)27)))) p=(a+b+3((ab))^(1/3) ((a)^(1/3) +(b)^(1/3) ))

$$\sqrt[{\mathrm{3}}]{\sqrt[{\mathrm{3}}]{\mathrm{2}}−\mathrm{1}}=\sqrt[{\mathrm{3}}]{{p}}+\sqrt[{\mathrm{3}}]{{c}} \\ $$$$\sqrt[{\mathrm{3}}]{\mathrm{2}}−\mathrm{1}={p}+{c}\:+\mathrm{3}\sqrt[{\mathrm{3}}]{{pc}}\left(\sqrt[{\mathrm{3}}]{{p}}+\sqrt[{\mathrm{3}}]{{c}}\right) \\ $$$$\sqrt[{\mathrm{3}}]{\mathrm{2}}−\mathrm{1}={p}+{c}+\mathrm{3}\sqrt[{\mathrm{3}}]{{pc}}\left(\sqrt[{\mathrm{3}}]{\sqrt[{\mathrm{3}}]{\mathrm{2}}−\mathrm{1}}\right) \\ $$$$\sqrt[{\mathrm{3}}]{\mathrm{2}}=\mathrm{3}\sqrt[{\mathrm{3}}]{{pc}}\left(\sqrt[{\mathrm{3}}]{\sqrt[{\mathrm{3}}]{\mathrm{2}}−\mathrm{1}}\right) \\ $$$$\mathrm{2}=\mathrm{27}{pc}\left(\sqrt[{\mathrm{3}}]{\mathrm{2}}−\mathrm{1}\right) \\ $$$${p}+{c}=−\mathrm{1}\Rightarrow{p}+\frac{\mathrm{2}}{\left(\sqrt[{\mathrm{3}}]{\mathrm{2}}−\mathrm{1}\right)\mathrm{27}{p}}=−\mathrm{1} \\ $$$${p}^{\mathrm{2}} +{p}+\frac{\mathrm{2}}{\left(\sqrt[{\mathrm{3}}]{\mathrm{2}}−\mathrm{1}\right)\mathrm{27}}=\mathrm{0} \\ $$$${p}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{1}−\frac{\mathrm{4}}{\left(\sqrt[{\mathrm{3}}]{\mathrm{2}}−\mathrm{1}\right)\mathrm{27}}}}{\mathrm{2}} \\ $$$${p}=−\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{1}−\frac{\mathrm{4}}{\left(\sqrt[{\mathrm{3}}]{\mathrm{2}}−\mathrm{1}\right)\mathrm{27}}}\: \\ $$$${c}=−\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{1}−\frac{\mathrm{4}}{\left(\sqrt[{\mathrm{3}}]{\mathrm{2}}−\mathrm{1}\right)\mathrm{27}}} \\ $$$${p}=\left({a}+{b}+\mathrm{3}\sqrt[{\mathrm{3}}]{{ab}}\left(\sqrt[{\mathrm{3}}]{{a}}+\sqrt[{\mathrm{3}}]{{b}}\right)\right) \\ $$$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com