
Question Number 123574 by shaker last updated on 26/Nov/20
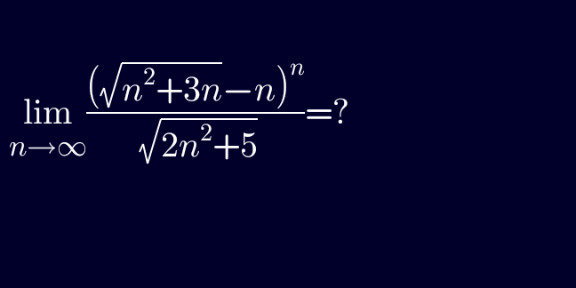
Answered by Olaf last updated on 26/Nov/20
![q(n) = ((((√(n^2 +3n))−n)^n )/( (√(2n^2 +5)))) lnq(n) = nln((√(n^2 +3n))−n)−(1/2)ln(2n^2 +5) lnq(n) = nln[n((√(1+(3/n)))−1)]−(1/2)ln[n^2 (2+(5/n^2 ))] lnq(n) = nlnn+nln((√(1+(3/n)))−1)−(1/2)lnn^2 −(1/2)ln(2+(5/n^2 )) lnq(n) = nln((√(1+(3/n)))−1)−(1/2)ln(2+(5/n^2 )) lnq(n) ∼_∞ nln(1+(3/(2n))−1)−(1/2)ln(2+(5/n^2 )) lnq(n) ∼_∞ nln((3/(2n)))−(1/2)ln(2+(5/n^2 )) lim_(n→∞) lnq(n) = +∞ ⇒ lim_(n→∞) q(n) = +∞](Q123584.png)
$${q}\left({n}\right)\:=\:\frac{\left(\sqrt{{n}^{\mathrm{2}} +\mathrm{3}{n}}−{n}\right)^{{n}} }{\:\sqrt{\mathrm{2}{n}^{\mathrm{2}} +\mathrm{5}}} \\ $$$$\mathrm{ln}{q}\left({n}\right)\:=\:{n}\mathrm{ln}\left(\sqrt{{n}^{\mathrm{2}} +\mathrm{3}{n}}−{n}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}{n}^{\mathrm{2}} +\mathrm{5}\right) \\ $$$$\mathrm{ln}{q}\left({n}\right)\:=\:{n}\mathrm{ln}\left[{n}\left(\sqrt{\mathrm{1}+\frac{\mathrm{3}}{{n}}}−\mathrm{1}\right)\right]−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left[{n}^{\mathrm{2}} \left(\mathrm{2}+\frac{\mathrm{5}}{{n}^{\mathrm{2}} }\right)\right] \\ $$$$\mathrm{ln}{q}\left({n}\right)\:=\:{n}\mathrm{ln}{n}+{n}\mathrm{ln}\left(\sqrt{\mathrm{1}+\frac{\mathrm{3}}{{n}}}−\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}{n}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}+\frac{\mathrm{5}}{{n}^{\mathrm{2}} }\right) \\ $$$$\mathrm{ln}{q}\left({n}\right)\:=\:{n}\mathrm{ln}\left(\sqrt{\mathrm{1}+\frac{\mathrm{3}}{{n}}}−\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}+\frac{\mathrm{5}}{{n}^{\mathrm{2}} }\right) \\ $$$$\mathrm{ln}{q}\left({n}\right)\:\underset{\infty} {\sim}\:{n}\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{3}}{\mathrm{2}{n}}−\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}+\frac{\mathrm{5}}{{n}^{\mathrm{2}} }\right) \\ $$$$\mathrm{ln}{q}\left({n}\right)\:\underset{\infty} {\sim}\:{n}\mathrm{ln}\left(\frac{\mathrm{3}}{\mathrm{2}{n}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}+\frac{\mathrm{5}}{{n}^{\mathrm{2}} }\right) \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}ln}{q}\left({n}\right)\:=\:+\infty \\ $$$$\Rightarrow\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}{q}\left({n}\right)\:=\:+\infty \\ $$
