Question and Answers Forum

All Questions      Topic List

Mensuration Questions

Previous in All Question      Next in All Question      

Previous in Mensuration      Next in Mensuration      

Question Number 123302 by peter frank last updated on 24/Nov/20

Answered by MJS_new last updated on 24/Nov/20

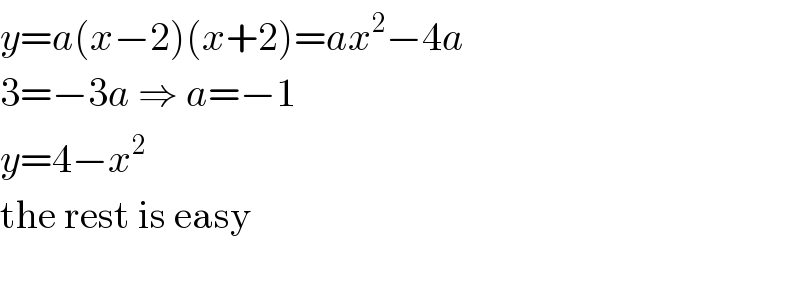
y=a(x−2)(x+2)=ax^2 −4a 3=−3a ⇒ a=−1 y=4−x^2 the rest is easy

$${y}={a}\left({x}−\mathrm{2}\right)\left({x}+\mathrm{2}\right)={ax}^{\mathrm{2}} −\mathrm{4}{a} \\ $$$$\mathrm{3}=−\mathrm{3}{a}\:\Rightarrow\:{a}=−\mathrm{1} \\ $$$${y}=\mathrm{4}−{x}^{\mathrm{2}} \\ $$$$\mathrm{the}\:\mathrm{rest}\:\mathrm{is}\:\mathrm{easy} \\ $$$$ \\ $$

Commented by peter frank last updated on 24/Nov/20

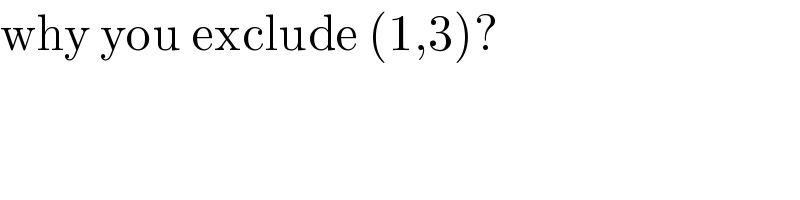
why you exclude (1,3)?

$$\mathrm{why}\:\mathrm{you}\:\mathrm{exclude}\:\left(\mathrm{1},\mathrm{3}\right)? \\ $$

Commented by MJS_new last updated on 24/Nov/20

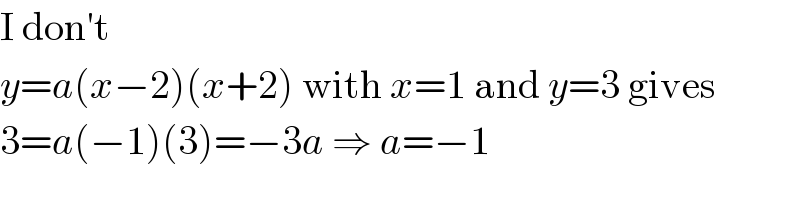
I don′t y=a(x−2)(x+2) with x=1 and y=3 gives 3=a(−1)(3)=−3a ⇒ a=−1

$$\mathrm{I}\:\mathrm{don}'\mathrm{t} \\ $$$${y}={a}\left({x}−\mathrm{2}\right)\left({x}+\mathrm{2}\right)\:\mathrm{with}\:{x}=\mathrm{1}\:\mathrm{and}\:{y}=\mathrm{3}\:\mathrm{gives} \\ $$$$\mathrm{3}={a}\left(−\mathrm{1}\right)\left(\mathrm{3}\right)=−\mathrm{3}{a}\:\Rightarrow\:{a}=−\mathrm{1} \\ $$

Commented by peter frank last updated on 24/Nov/20

sorry sir explain first line

$$\mathrm{sorry}\:\mathrm{sir}\:\mathrm{explain}\:\mathrm{first}\:\mathrm{line} \\ $$

Commented by MJS_new last updated on 24/Nov/20

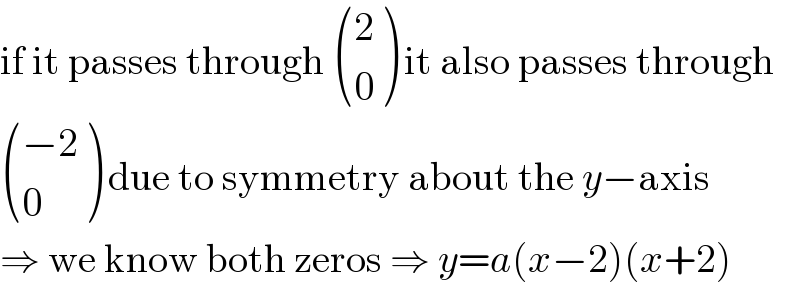
if it passes through ((2),(0) ) it also passes through (((−2)),(0) ) due to symmetry about the y−axis ⇒ we know both zeros ⇒ y=a(x−2)(x+2)

$$\mathrm{if}\:\mathrm{it}\:\mathrm{passes}\:\mathrm{through}\:\begin{pmatrix}{\mathrm{2}}\\{\mathrm{0}}\end{pmatrix}\:\mathrm{it}\:\mathrm{also}\:\mathrm{passes}\:\mathrm{through} \\ $$$$\begin{pmatrix}{−\mathrm{2}}\\{\mathrm{0}}\end{pmatrix}\:\mathrm{due}\:\mathrm{to}\:\mathrm{symmetry}\:\mathrm{about}\:\mathrm{the}\:{y}−\mathrm{axis} \\ $$$$\Rightarrow\:\mathrm{we}\:\mathrm{know}\:\mathrm{both}\:\mathrm{zeros}\:\Rightarrow\:{y}={a}\left({x}−\mathrm{2}\right)\left({x}+\mathrm{2}\right) \\ $$

Answered by MJS_new last updated on 24/Nov/20

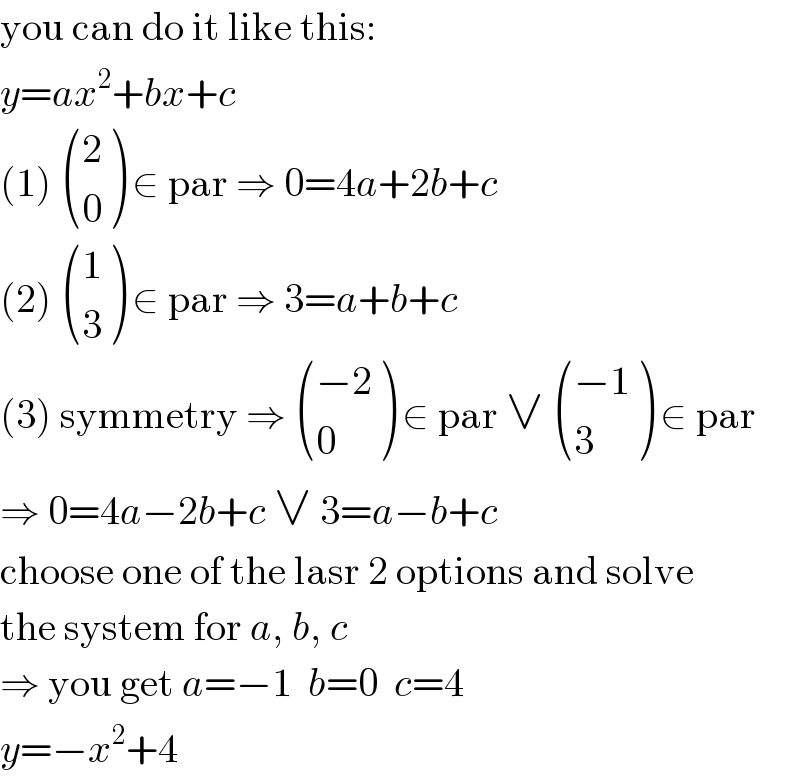
you can do it like this: y=ax^2 +bx+c (1) ((2),(0) ) ∈ par ⇒ 0=4a+2b+c (2) ((1),(3) ) ∈ par ⇒ 3=a+b+c (3) symmetry ⇒ (((−2)),(0) ) ∈ par ∨ (((−1)),(3) ) ∈ par ⇒ 0=4a−2b+c ∨ 3=a−b+c choose one of the lasr 2 options and solve the system for a, b, c ⇒ you get a=−1 b=0 c=4 y=−x^2 +4

$$\mathrm{you}\:\mathrm{can}\:\mathrm{do}\:\mathrm{it}\:\mathrm{like}\:\mathrm{this}: \\ $$$${y}={ax}^{\mathrm{2}} +{bx}+{c} \\ $$$$\left(\mathrm{1}\right)\:\begin{pmatrix}{\mathrm{2}}\\{\mathrm{0}}\end{pmatrix}\:\in\:\mathrm{par}\:\Rightarrow\:\mathrm{0}=\mathrm{4}{a}+\mathrm{2}{b}+{c} \\ $$$$\left(\mathrm{2}\right)\:\begin{pmatrix}{\mathrm{1}}\\{\mathrm{3}}\end{pmatrix}\:\in\:\mathrm{par}\:\Rightarrow\:\mathrm{3}={a}+{b}+{c} \\ $$$$\left(\mathrm{3}\right)\:\mathrm{symmetry}\:\Rightarrow\:\begin{pmatrix}{−\mathrm{2}}\\{\mathrm{0}}\end{pmatrix}\:\in\:\mathrm{par}\:\vee\:\begin{pmatrix}{−\mathrm{1}}\\{\mathrm{3}}\end{pmatrix}\:\in\:\mathrm{par} \\ $$$$\Rightarrow\:\mathrm{0}=\mathrm{4}{a}−\mathrm{2}{b}+{c}\:\vee\:\mathrm{3}={a}−{b}+{c} \\ $$$$\mathrm{choose}\:\mathrm{one}\:\mathrm{of}\:\mathrm{the}\:\mathrm{lasr}\:\mathrm{2}\:\mathrm{options}\:\mathrm{and}\:\mathrm{solve} \\ $$$$\mathrm{the}\:\mathrm{system}\:\mathrm{for}\:{a},\:{b},\:{c} \\ $$$$\Rightarrow\:\mathrm{you}\:\mathrm{get}\:{a}=−\mathrm{1}\:\:{b}=\mathrm{0}\:\:{c}=\mathrm{4} \\ $$$${y}=−{x}^{\mathrm{2}} +\mathrm{4} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com