
Question Number 123027 by Lekhraj last updated on 21/Nov/20

Commented by kolos last updated on 24/Nov/20
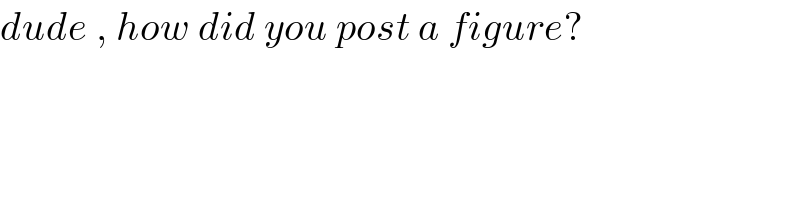
$${dude}\:,\:{how}\:{did}\:{you}\:{post}\:{a}\:{figure}?\: \\ $$
Answered by TANMAY PANACEA last updated on 21/Nov/20

$${AC}={y} \\ $$$${BC}={x} \\ $$$$\left({AC}\right)^{\mathrm{2}} +\left({BC}\right)^{\mathrm{2}} =\left({AB}\right)^{\mathrm{2}} \\ $$$${angle}\:<{ABC}=\theta\:\:{AB}={hypotsneous} \\ $$$${AC}={perpendicular}\:\:\:{BC}={base} \\ $$$${tan}\theta=\frac{{AC}}{{BC}}\:\:\:\:\:{tan}\left(\mathrm{90}−\theta\right)=\frac{{BC}}{{AC}} \\ $$$${sin}\theta=\frac{{CD}}{{BC}}\:\:\:\:{sin}\left(\mathrm{90}−\theta\right)=\frac{{CD}}{{AC}} \\ $$$${sin}^{\mathrm{2}} \theta+{cos}^{\mathrm{2}} \theta=\mathrm{1} \\ $$$$\frac{{CD}^{\mathrm{2}} }{{BC}^{\mathrm{2}} }+\frac{{CD}^{\mathrm{2}} }{{AC}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\frac{\mathrm{1}}{{BC}^{\mathrm{2}} }+\frac{\mathrm{1}}{{AC}^{\mathrm{2}} }=\frac{\mathrm{1}}{{CD}^{\mathrm{2}} } \\ $$$$ \\ $$
Answered by Olaf last updated on 21/Nov/20
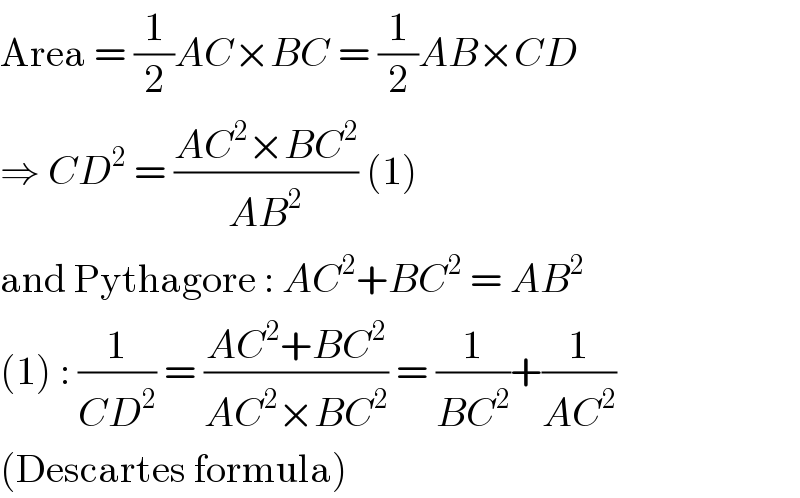
$$\mathrm{Area}\:=\:\frac{\mathrm{1}}{\mathrm{2}}{AC}×{BC}\:=\:\frac{\mathrm{1}}{\mathrm{2}}{AB}×{CD} \\ $$$$\Rightarrow\:{CD}^{\mathrm{2}} \:=\:\frac{{AC}^{\mathrm{2}} ×{BC}^{\mathrm{2}} }{{AB}^{\mathrm{2}} }\:\left(\mathrm{1}\right) \\ $$$$\mathrm{and}\:\mathrm{Pythagore}\::\:{AC}^{\mathrm{2}} +{BC}^{\mathrm{2}} \:=\:{AB}^{\mathrm{2}} \\ $$$$\left(\mathrm{1}\right)\::\:\frac{\mathrm{1}}{{CD}^{\mathrm{2}} }\:=\:\frac{{AC}^{\mathrm{2}} +{BC}^{\mathrm{2}} }{{AC}^{\mathrm{2}} ×{BC}^{\mathrm{2}} }\:=\:\frac{\mathrm{1}}{{BC}^{\mathrm{2}} }+\frac{\mathrm{1}}{{AC}^{\mathrm{2}} } \\ $$$$\left(\mathrm{Descartes}\:\mathrm{formula}\right) \\ $$
