
Question Number 122828 by bemath last updated on 20/Nov/20

Answered by bobhans last updated on 20/Nov/20
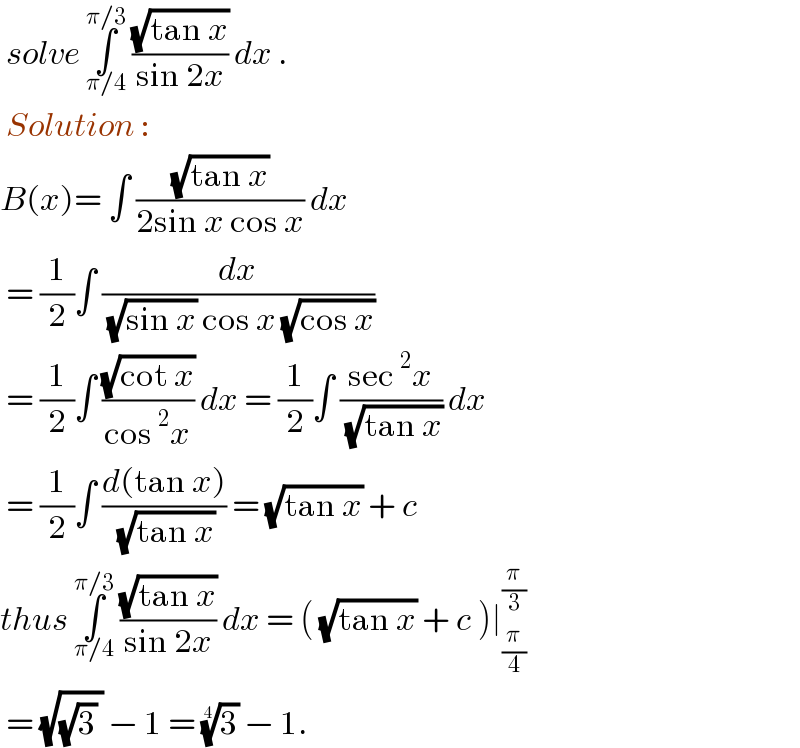
$$\:{solve}\:\underset{\pi/\mathrm{4}} {\overset{\pi/\mathrm{3}} {\int}}\:\frac{\sqrt{\mathrm{tan}\:{x}}}{\mathrm{sin}\:\mathrm{2}{x}}\:{dx}\:.\: \\ $$$$\:{Solution}\::\: \\ $$$${B}\left({x}\right)=\:\int\:\frac{\sqrt{\mathrm{tan}\:{x}}}{\mathrm{2sin}\:{x}\:\mathrm{cos}\:{x}}\:{dx}\: \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{{dx}}{\:\sqrt{\mathrm{sin}\:{x}}\:\mathrm{cos}\:{x}\:\sqrt{\mathrm{cos}\:{x}}} \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\sqrt{\mathrm{cot}\:{x}}}{\mathrm{cos}\:^{\mathrm{2}} {x}}\:{dx}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{sec}\:^{\mathrm{2}} {x}}{\:\sqrt{\mathrm{tan}\:{x}}}\:{dx} \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{{d}\left(\mathrm{tan}\:{x}\right)}{\:\sqrt{\mathrm{tan}\:{x}}}\:=\:\sqrt{\mathrm{tan}\:{x}}\:+\:{c}\: \\ $$$${thus}\:\underset{\pi/\mathrm{4}} {\overset{\pi/\mathrm{3}} {\int}}\:\frac{\sqrt{\mathrm{tan}\:{x}}}{\mathrm{sin}\:\mathrm{2}{x}}\:{dx}\:=\:\left(\:\sqrt{\mathrm{tan}\:{x}}\:+\:{c}\:\right)\mid_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{3}}} \\ $$$$\:=\:\sqrt{\sqrt{\mathrm{3}}\:}\:−\:\mathrm{1}\:=\:\sqrt[{\mathrm{4}}]{\mathrm{3}}\:−\:\mathrm{1}.\:\: \\ $$
