
Question Number 122572 by rs4089 last updated on 18/Nov/20
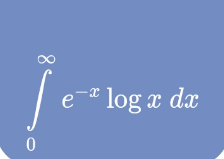
Answered by Olaf last updated on 18/Nov/20

$$\mathrm{With}\:\mathrm{Euler}'\mathrm{s}\:\mathrm{Gamma}\:\mathrm{function}\:\Gamma\:: \\ $$$$\int_{\mathrm{0}} ^{\infty} {e}^{−{x}} \mathrm{ln}{xdx}\:=\:\Gamma'\left(\mathrm{1}\right)\:=\:−\gamma \\ $$$$\mathrm{where}\:\gamma\:\mathrm{is}\:\mathrm{the}\:\mathrm{Euler}−\mathrm{Mascheroni} \\ $$$$\mathrm{constant}\::\:\gamma\:\approx\:\mathrm{0}.\mathrm{5772156649} \\ $$
