
Question Number 122216 by help last updated on 14/Nov/20
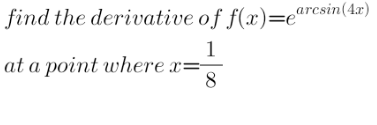
Answered by liberty last updated on 14/Nov/20
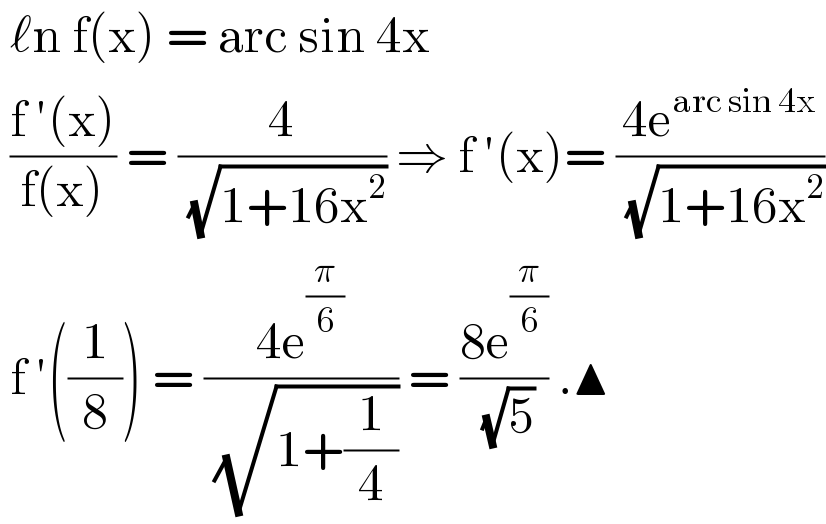
$$\:\ell\mathrm{n}\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\mathrm{arc}\:\mathrm{sin}\:\mathrm{4x}\: \\ $$$$\:\frac{\mathrm{f}\:'\left(\mathrm{x}\right)}{\mathrm{f}\left(\mathrm{x}\right)}\:=\:\frac{\mathrm{4}}{\:\sqrt{\mathrm{1}+\mathrm{16x}^{\mathrm{2}} }}\:\Rightarrow\:\mathrm{f}\:'\left(\mathrm{x}\right)=\:\frac{\mathrm{4e}^{\mathrm{arc}\:\mathrm{sin}\:\mathrm{4x}} }{\:\sqrt{\mathrm{1}+\mathrm{16x}^{\mathrm{2}} }} \\ $$$$\:\mathrm{f}\:'\left(\frac{\mathrm{1}}{\mathrm{8}}\right)\:=\:\frac{\mathrm{4e}^{\frac{\pi}{\mathrm{6}}} }{\:\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}}}\:=\:\frac{\mathrm{8e}^{\frac{\pi}{\mathrm{6}}} }{\:\sqrt{\mathrm{5}}}\:.\blacktriangle\: \\ $$
Commented by help last updated on 14/Nov/20

$${last}\:{step}\:{please}. \\ $$$${explain} \\ $$
Commented by liberty last updated on 15/Nov/20
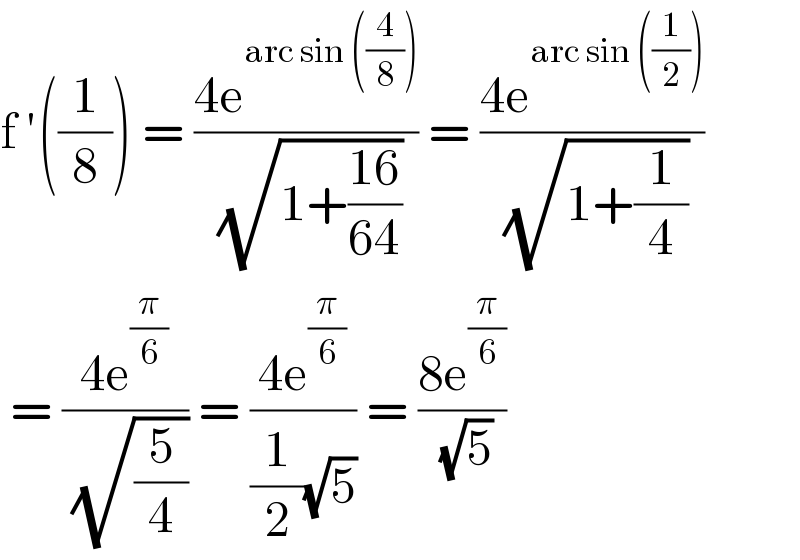
$$\mathrm{f}\:'\left(\frac{\mathrm{1}}{\mathrm{8}}\right)\:=\:\frac{\mathrm{4e}^{\mathrm{arc}\:\mathrm{sin}\:\left(\frac{\mathrm{4}}{\mathrm{8}}\right)} }{\:\sqrt{\mathrm{1}+\frac{\mathrm{16}}{\mathrm{64}}}}\:=\:\frac{\mathrm{4e}^{\mathrm{arc}\:\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} }{\:\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}}} \\ $$$$\:=\:\frac{\mathrm{4e}^{\frac{\pi}{\mathrm{6}}} }{\:\sqrt{\frac{\mathrm{5}}{\mathrm{4}}}}\:=\:\frac{\mathrm{4e}^{\frac{\pi}{\mathrm{6}}} }{\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{5}}}\:=\:\frac{\mathrm{8e}^{\frac{\pi}{\mathrm{6}}} }{\:\sqrt{\mathrm{5}}} \\ $$
