
Question Number 122047 by help last updated on 13/Nov/20
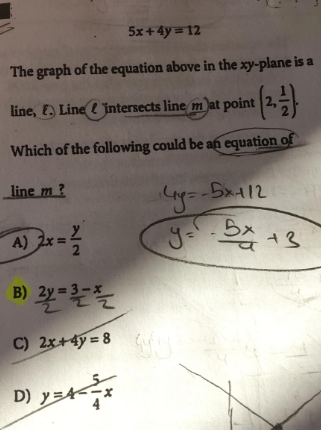
Answered by TANMAY PANACEA last updated on 13/Nov/20

$$\mathrm{5}{x}+\mathrm{4}{y}=\mathrm{12} \\ $$$$\frac{{x}}{\mathrm{2}.\mathrm{4}}+\frac{{y}}{\mathrm{3}}=\mathrm{1} \\ $$$${line}\:{l}\:{and}\:{m}\:{intersect}\:{at}\:{point}\:{m}\left(\mathrm{2},\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$${eqn}\:{of}\:{line}\:{m}\:\left({y}−\mathrm{0}.\mathrm{5}\right)=\left({tan}\theta\right)\left({x}−\mathrm{2}\right) \\ $$$$\left({y}−\frac{\mathrm{1}}{\mathrm{2}}\right)=\left({tan}\theta\right)\left({x}−\mathrm{2}\right) \\ $$$${y}=\left({tan}\theta\right){x}−\mathrm{2}{tan}\theta+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${here}\:{option}\:{be}\:{is}\:{satisfied}\:{by}\:\left(\mathrm{2},\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\mathrm{2}{y}=\mathrm{3}−{x} \\ $$
