
Question Number 121909 by help last updated on 12/Nov/20
Answered by mr W last updated on 13/Nov/20
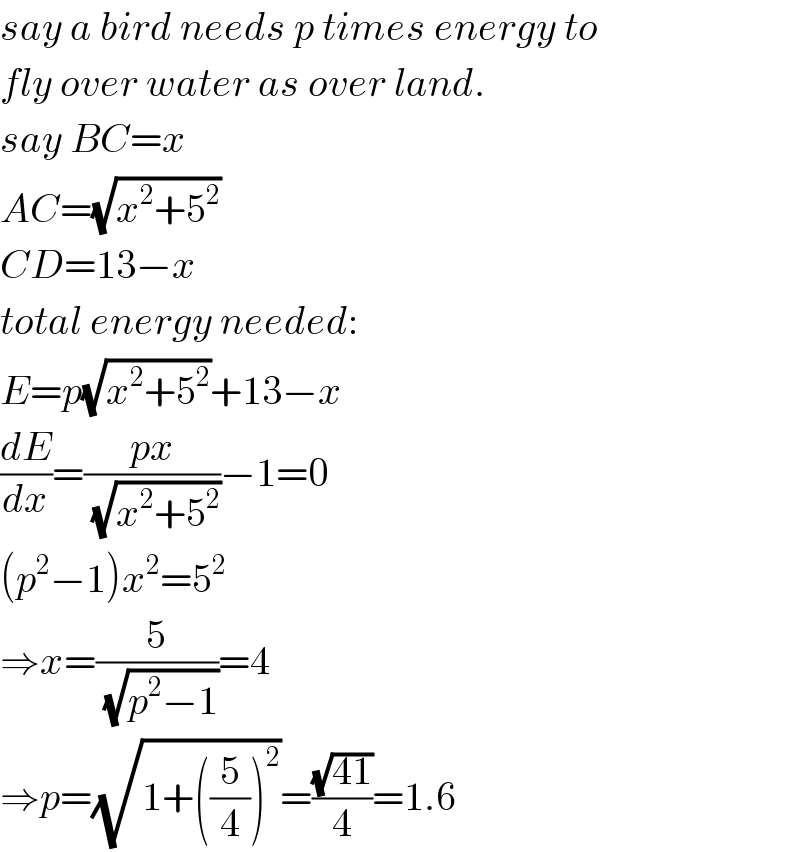
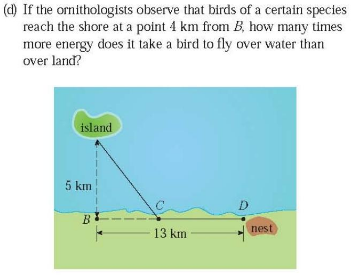
$${say}\:{a}\:{bird}\:{needs}\:{p}\:{times}\:{energy}\:{to} \\ $$$${fly}\:{over}\:{water}\:{as}\:{over}\:{land}. \\ $$$${say}\:{BC}={x} \\ $$$${AC}=\sqrt{{x}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} } \\ $$$${CD}=\mathrm{13}−{x} \\ $$$${total}\:{energy}\:{needed}: \\ $$$${E}={p}\sqrt{{x}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} }+\mathrm{13}−{x} \\ $$$$\frac{{dE}}{{dx}}=\frac{{px}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} }}−\mathrm{1}=\mathrm{0} \\ $$$$\left({p}^{\mathrm{2}} −\mathrm{1}\right){x}^{\mathrm{2}} =\mathrm{5}^{\mathrm{2}} \\ $$$$\Rightarrow{x}=\frac{\mathrm{5}}{\:\sqrt{{p}^{\mathrm{2}} −\mathrm{1}}}=\mathrm{4} \\ $$$$\Rightarrow{p}=\sqrt{\mathrm{1}+\left(\frac{\mathrm{5}}{\mathrm{4}}\right)^{\mathrm{2}} }=\frac{\sqrt{\mathrm{41}}}{\mathrm{4}}=\mathrm{1}.\mathrm{6} \\ $$
