
Question Number 121817 by shaker last updated on 12/Nov/20
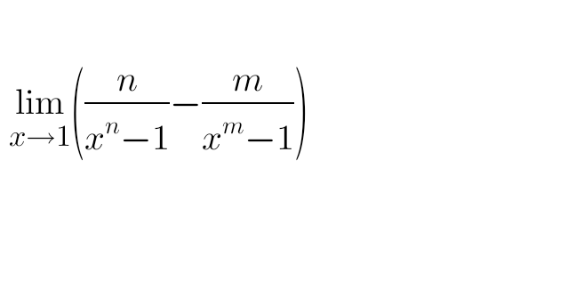
Answered by liberty last updated on 12/Nov/20
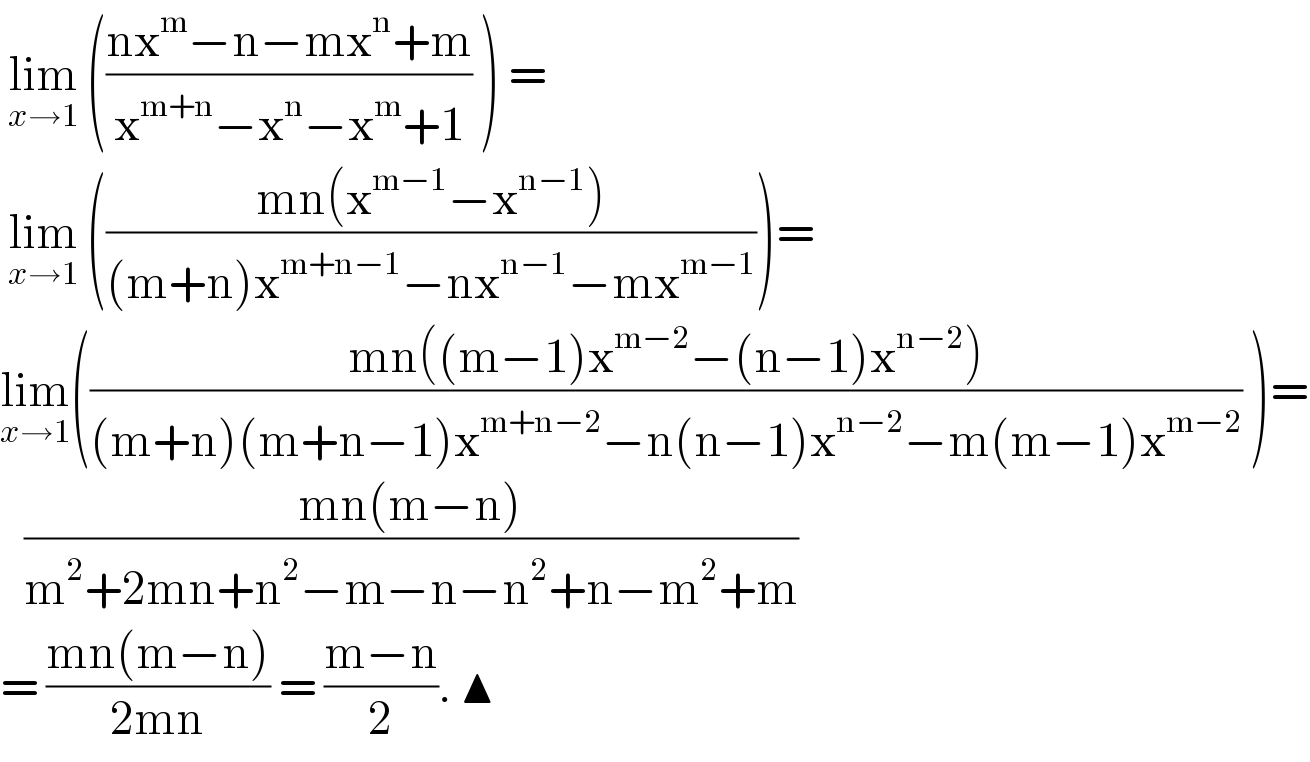
$$\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\left(\frac{\mathrm{nx}^{\mathrm{m}} −\mathrm{n}−\mathrm{mx}^{\mathrm{n}} +\mathrm{m}}{\mathrm{x}^{\mathrm{m}+\mathrm{n}} −\mathrm{x}^{\mathrm{n}} −\mathrm{x}^{\mathrm{m}} +\mathrm{1}}\:\right)\:=\: \\ $$$$\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\left(\frac{\mathrm{mn}\left(\mathrm{x}^{\mathrm{m}−\mathrm{1}} −\mathrm{x}^{\mathrm{n}−\mathrm{1}} \right)}{\left(\mathrm{m}+\mathrm{n}\right)\mathrm{x}^{\mathrm{m}+\mathrm{n}−\mathrm{1}} −\mathrm{nx}^{\mathrm{n}−\mathrm{1}} −\mathrm{mx}^{\mathrm{m}−\mathrm{1}} }\right)= \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\left(\frac{\mathrm{mn}\left(\left(\mathrm{m}−\mathrm{1}\right)\mathrm{x}^{\mathrm{m}−\mathrm{2}} −\left(\mathrm{n}−\mathrm{1}\right)\mathrm{x}^{\mathrm{n}−\mathrm{2}} \right)}{\left(\mathrm{m}+\mathrm{n}\right)\left(\mathrm{m}+\mathrm{n}−\mathrm{1}\right)\mathrm{x}^{\mathrm{m}+\mathrm{n}−\mathrm{2}} −\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\mathrm{x}^{\mathrm{n}−\mathrm{2}} −\mathrm{m}\left(\mathrm{m}−\mathrm{1}\right)\mathrm{x}^{\mathrm{m}−\mathrm{2}} }\:\right)= \\ $$$$\:\:\:\frac{\mathrm{mn}\left(\mathrm{m}−\mathrm{n}\right)}{\mathrm{m}^{\mathrm{2}} +\mathrm{2mn}+\mathrm{n}^{\mathrm{2}} −\mathrm{m}−\mathrm{n}−\mathrm{n}^{\mathrm{2}} +\mathrm{n}−\mathrm{m}^{\mathrm{2}} +\mathrm{m}} \\ $$$$=\:\frac{\mathrm{mn}\left(\mathrm{m}−\mathrm{n}\right)}{\mathrm{2mn}}\:=\:\frac{\mathrm{m}−\mathrm{n}}{\mathrm{2}}.\:\blacktriangle \\ $$
Answered by bemath last updated on 12/Nov/20

$${let}\:{x}\:=\:\mathrm{1}+\:{w}\:;\:{w}\rightarrow\mathrm{0} \\ $$$$\:\underset{{w}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{{n}}{\left(\mathrm{1}+{w}\right)^{{n}} −\mathrm{1}}\:−\:\frac{{m}}{\left(\mathrm{1}+{w}\right)^{{m}} −\mathrm{1}}\right) \\ $$$$=\:\underset{{w}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{{n}}{{nw}+\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}}{w}^{\mathrm{2}} }\:−\:\frac{{m}}{{mw}+\frac{{m}\left({m}−\mathrm{1}\right)}{\mathrm{2}}{w}^{\mathrm{2}} }\right) \\ $$$$=\:\underset{{w}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{2}{n}}{\mathrm{2}{nw}+{n}\left({n}−\mathrm{1}\right){w}^{\mathrm{2}} }\:−\:\frac{\mathrm{2}{m}}{\mathrm{2}{mw}+{m}\left({m}−\mathrm{1}\right){w}^{\mathrm{2}} }\right) \\ $$$$=\:\underset{{w}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{2}{n}\left(\mathrm{2}{mw}+{m}\left({m}−\mathrm{1}\right){w}^{\mathrm{2}} \right)−\mathrm{2}{m}\left(\mathrm{2}{nw}+{n}\left({n}−\mathrm{1}\right){w}^{\mathrm{2}} \right)}{\left(\mathrm{2}{nw}+{n}\left({n}−\mathrm{1}\right){w}^{\mathrm{2}} \right)\left(\mathrm{2}{mw}+{m}\left({m}−\mathrm{1}\right){w}^{\mathrm{2}} \right)}\right) \\ $$$$=\:\underset{{w}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{4}{mn}+\mathrm{2}{mn}\left({m}−\mathrm{1}\right){w}−\mathrm{4}{mn}−\mathrm{2}{mn}\left({n}−\mathrm{1}\right){w}}{\left(\mathrm{2}{n}+{n}\left({n}−\mathrm{1}\right){w}\right)\left(\mathrm{2}{mw}+{m}\left({m}−\mathrm{1}\right){w}^{\mathrm{2}} \right)}\right) \\ $$$$=\:\underset{{w}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\left(\mathrm{2}{mn}\left({m}−\mathrm{1}\right)−\mathrm{2}{mn}\left({n}−\mathrm{1}\right)\right){w}}{\left(\mathrm{2}{n}+{n}\left({n}−\mathrm{1}\right){w}\right)\left(\mathrm{2}{m}+{m}\left({m}−\mathrm{1}\right){w}\right){w}}\right) \\ $$$$=\:\underset{{w}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{2}{mn}\left({m}−\mathrm{1}−{n}+\mathrm{1}\right)}{\left(\mathrm{2}{n}+{n}\left({n}−\mathrm{1}\right){w}\right)\left(\mathrm{2}{m}+{m}\left({m}−\mathrm{1}\right){w}\right)}\right. \\ $$$$=\:\underset{{w}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{2}{mn}.\left({m}−{n}\right)}{\mathrm{2}{n}.\mathrm{2}{m}}\right)\:=\:\frac{{m}−{n}}{\mathrm{2}} \\ $$
