
Question Number 121677 by TITA last updated on 10/Nov/20

Commented by TITA last updated on 10/Nov/20

$${please}\:{help} \\ $$
Answered by MJS_new last updated on 11/Nov/20

$$\left.\mathrm{1}\right) \\ $$$${n}!=\mathrm{1}×\mathrm{2}×\mathrm{3}×\mathrm{4}×\mathrm{5}×...×{n} \\ $$$$\Rightarrow\:\mathrm{all}\:\mathrm{primes}\:\leqslant{n}\:\mathrm{divide}\:{n}! \\ $$$$\Leftrightarrow\:\mathrm{for}\:\mathrm{any}\:\mathrm{given}\:\mathrm{prime}\:{p}\leqslant{n}\:\mathrm{we}\:\mathrm{have}\:{n}!={k}_{{p}} ×{p} \\ $$$$\:\:\:\:\:\:\:\mathrm{with}\:{k}_{{p}} \in\mathbb{N} \\ $$$$\Rightarrow\:{n}!+\mathrm{1}={k}_{{p}} ×{p}+\mathrm{1}\:\mathrm{which}\:\mathrm{cannot}\:\mathrm{be}\:\mathrm{divisible} \\ $$$$\:\:\:\:\:\mathrm{by}\:{p}\:\mathrm{for}\:\mathrm{any}\:{p}\leqslant{n} \\ $$$$\Rightarrow\:\mathrm{if}\:{n}\:\mathrm{is}\:\mathrm{prime}\:\Rightarrow\:{n}!+\mathrm{1}\:\mathrm{is}\:\mathrm{not}\:\mathrm{divisible}\:\mathrm{by}\:{n} \\ $$$$\:\:\:\:\:\mathrm{nor}\:\mathrm{any}\:\mathrm{other}\:{p}\leqslant{n}\:\Rightarrow\:\mathrm{there}\:\mathrm{is}\:\mathrm{at}\:\mathrm{least}\:\mathrm{one} \\ $$$$\:\:\:\:\:\mathrm{prime}>{n} \\ $$
Answered by MJS_new last updated on 11/Nov/20
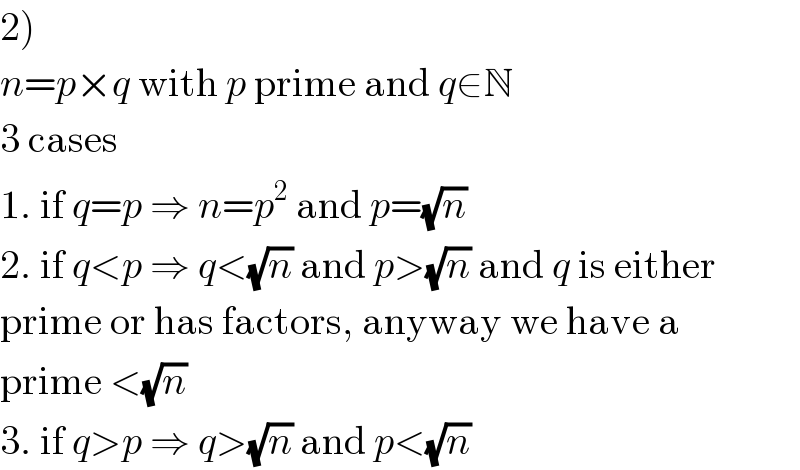
$$\left.\mathrm{2}\right) \\ $$$${n}={p}×{q}\:\mathrm{with}\:{p}\:\mathrm{prime}\:\mathrm{and}\:{q}\in\mathbb{N} \\ $$$$\mathrm{3}\:\mathrm{cases} \\ $$$$\mathrm{1}.\:\mathrm{if}\:{q}={p}\:\Rightarrow\:{n}={p}^{\mathrm{2}} \:\mathrm{and}\:{p}=\sqrt{{n}} \\ $$$$\mathrm{2}.\:\mathrm{if}\:{q}<{p}\:\Rightarrow\:{q}<\sqrt{{n}}\:\mathrm{and}\:{p}>\sqrt{{n}}\:\mathrm{and}\:{q}\:\mathrm{is}\:\mathrm{either} \\ $$$$\mathrm{prime}\:\mathrm{or}\:\mathrm{has}\:\mathrm{factors},\:\mathrm{anyway}\:\mathrm{we}\:\mathrm{have}\:\mathrm{a} \\ $$$$\mathrm{prime}\:<\sqrt{{n}} \\ $$$$\mathrm{3}.\:\mathrm{if}\:{q}>{p}\:\Rightarrow\:{q}>\sqrt{{n}}\:\mathrm{and}\:{p}<\sqrt{{n}} \\ $$
