
Question Number 121553 by I want to learn more last updated on 09/Nov/20
Commented by I want to learn more last updated on 09/Nov/20

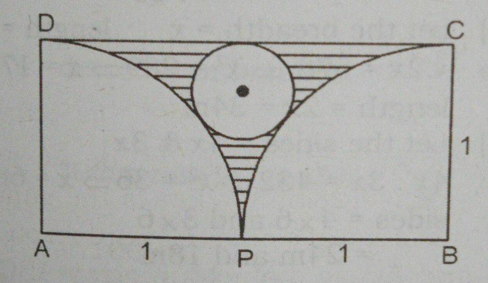
$$\mathrm{Area}\:\mathrm{of}\:\mathrm{shaded} \\ $$
Answered by TANMAY PANACEA last updated on 09/Nov/20
![Let A(0,0) B(2,0) D(0,1) C(2,1) eqn AB=x axis AD=yaxis centre small circle(1,k) radius=r k+r=1 (1−0)^2 +(k−0)^2 =(1+r)^2 [distance between centre A and centre of small circle] 1+(1−r)^2 =1+2r+r^2 1+1−2r+r^2 =1+2r+r^2 4r=1→r=(1/4) shaded area. 2×1−2×(1/4)×π1^2 −π×((1/4))^2 =2−(π/2)−(π/(16))= =((32−8π−π)/(16))=((32−9π)/(16))](Q121556.png)
$${Let}\:{A}\left(\mathrm{0},\mathrm{0}\right)\:\:{B}\left(\mathrm{2},\mathrm{0}\right)\:{D}\left(\mathrm{0},\mathrm{1}\right)\:\:{C}\left(\mathrm{2},\mathrm{1}\right) \\ $$$${eqn}\:{AB}={x}\:{axis}\:\:{AD}={yaxis} \\ $$$${centre}\:{small}\:{circle}\left(\mathrm{1},{k}\right)\:{radius}={r} \\ $$$${k}+{r}=\mathrm{1} \\ $$$$\left(\mathrm{1}−\mathrm{0}\right)^{\mathrm{2}} +\left({k}−\mathrm{0}\right)^{\mathrm{2}} =\left(\mathrm{1}+{r}\right)^{\mathrm{2}} \:\left[{distance}\:{between}\right. \\ $$$$\left.{centre}\:{A}\:{and}\:{centre}\:{of}\:{small}\:{circle}\right] \\ $$$$\mathrm{1}+\left(\mathrm{1}−{r}\right)^{\mathrm{2}} =\mathrm{1}+\mathrm{2}{r}+{r}^{\mathrm{2}} \\ $$$$\mathrm{1}+\mathrm{1}−\mathrm{2}{r}+{r}^{\mathrm{2}} =\mathrm{1}+\mathrm{2}{r}+{r}^{\mathrm{2}} \\ $$$$\mathrm{4}{r}=\mathrm{1}\rightarrow{r}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\boldsymbol{{shaded}}\:\boldsymbol{{area}}. \\ $$$$\mathrm{2}×\mathrm{1}−\mathrm{2}×\frac{\mathrm{1}}{\mathrm{4}}×\pi\mathrm{1}^{\mathrm{2}} −\pi×\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} \\ $$$$=\mathrm{2}−\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{16}}= \\ $$$$=\frac{\mathrm{32}−\mathrm{8}\pi−\pi}{\mathrm{16}}=\frac{\mathrm{32}−\mathrm{9}\pi}{\mathrm{16}} \\ $$$$ \\ $$
Commented by I want to learn more last updated on 09/Nov/20

$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$
Commented by TANMAY PANACEA last updated on 09/Nov/20

$${most}\:{welcome} \\ $$
Answered by mr W last updated on 09/Nov/20
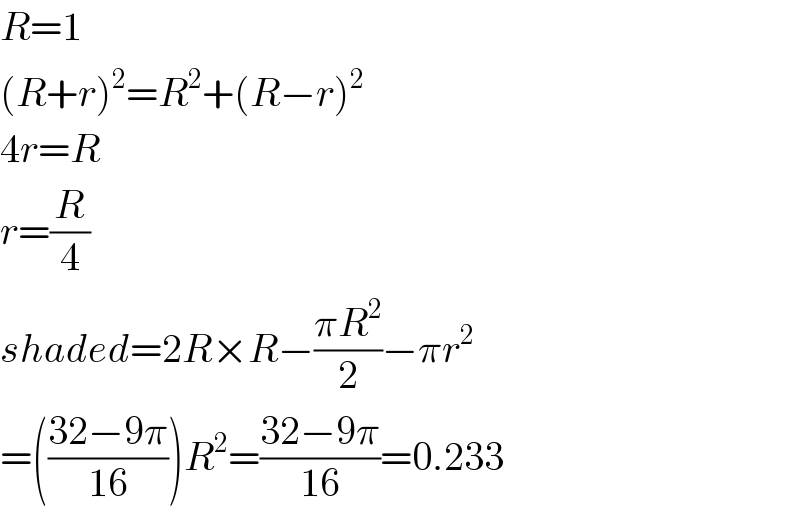
$${R}=\mathrm{1} \\ $$$$\left({R}+{r}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} +\left({R}−{r}\right)^{\mathrm{2}} \\ $$$$\mathrm{4}{r}={R} \\ $$$${r}=\frac{{R}}{\mathrm{4}} \\ $$$${shaded}=\mathrm{2}{R}×{R}−\frac{\pi{R}^{\mathrm{2}} }{\mathrm{2}}−\pi{r}^{\mathrm{2}} \\ $$$$=\left(\frac{\mathrm{32}−\mathrm{9}\pi}{\mathrm{16}}\right){R}^{\mathrm{2}} =\frac{\mathrm{32}−\mathrm{9}\pi}{\mathrm{16}}=\mathrm{0}.\mathrm{233} \\ $$
Commented by I want to learn more last updated on 10/Nov/20

$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{sir} \\ $$
Commented by I want to learn more last updated on 10/Nov/20

$$\mathrm{Sir},\:\mathrm{help}\:\mathrm{me}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{permutation}\:\:\:\:\mathrm{Q}\:\mathrm{121552} \\ $$
