
Question Number 121538 by Khalmohmmad last updated on 09/Nov/20
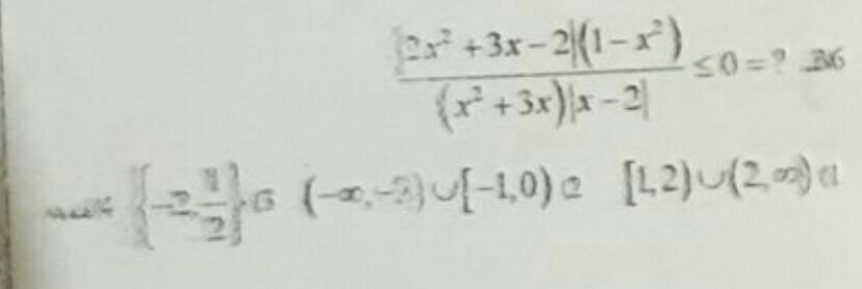
Answered by benjo_mathlover last updated on 09/Nov/20
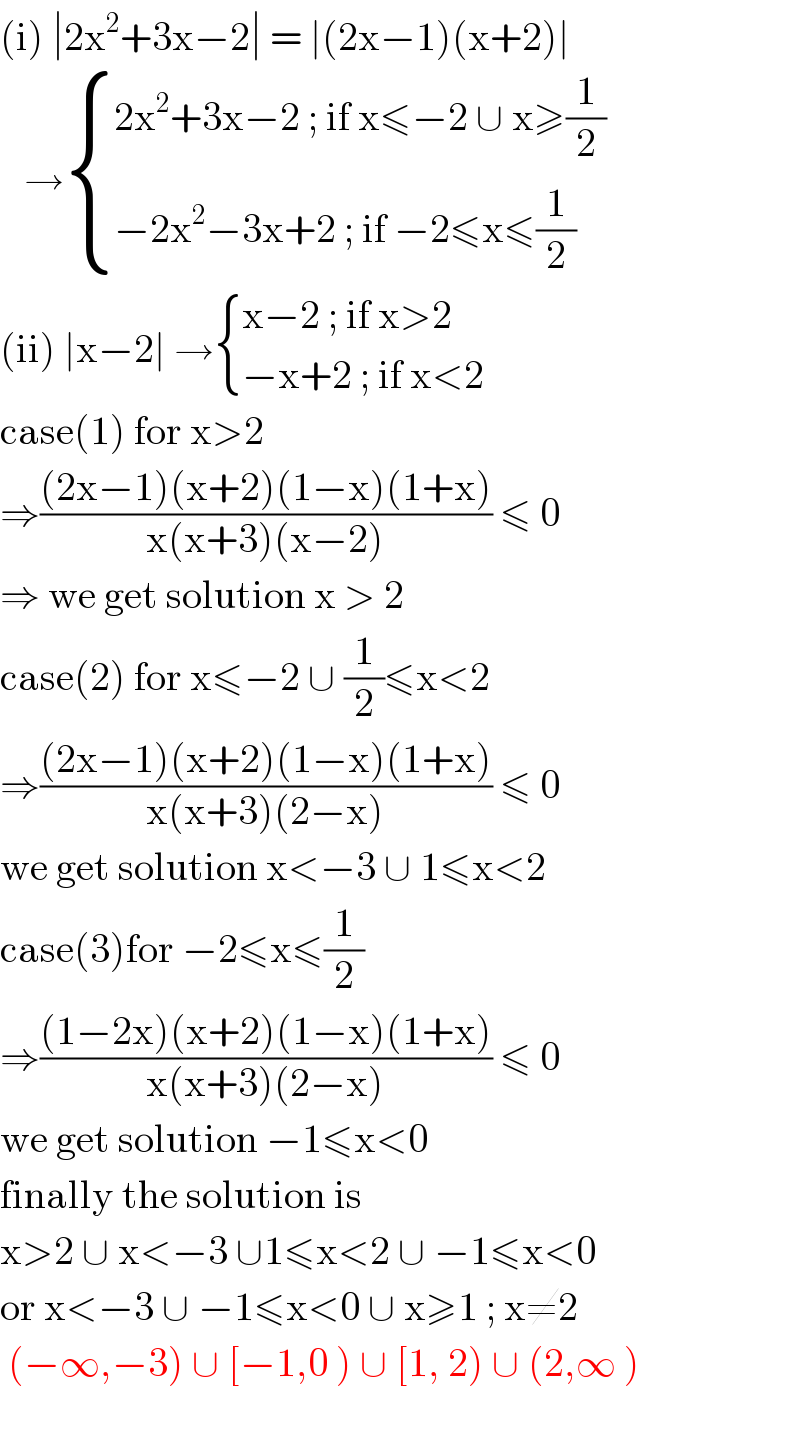
$$\left(\mathrm{i}\right)\:\mid\mathrm{2x}^{\mathrm{2}} +\mathrm{3x}−\mathrm{2}\mid\:=\:\mid\left(\mathrm{2x}−\mathrm{1}\right)\left(\mathrm{x}+\mathrm{2}\right)\mid \\ $$$$\:\:\:\rightarrow\begin{cases}{\mathrm{2x}^{\mathrm{2}} +\mathrm{3x}−\mathrm{2}\:;\:\mathrm{if}\:\mathrm{x}\leqslant−\mathrm{2}\:\cup\:\mathrm{x}\geqslant\frac{\mathrm{1}}{\mathrm{2}}}\\{−\mathrm{2x}^{\mathrm{2}} −\mathrm{3x}+\mathrm{2}\:;\:\mathrm{if}\:−\mathrm{2}\leqslant\mathrm{x}\leqslant\frac{\mathrm{1}}{\mathrm{2}}}\end{cases} \\ $$$$\left(\mathrm{ii}\right)\:\mid\mathrm{x}−\mathrm{2}\mid\:\rightarrow\begin{cases}{\mathrm{x}−\mathrm{2}\:;\:\mathrm{if}\:\mathrm{x}>\mathrm{2}}\\{−\mathrm{x}+\mathrm{2}\:;\:\mathrm{if}\:\mathrm{x}<\mathrm{2}}\end{cases} \\ $$$$\mathrm{case}\left(\mathrm{1}\right)\:\mathrm{for}\:\mathrm{x}>\mathrm{2}\: \\ $$$$\Rightarrow\frac{\left(\mathrm{2x}−\mathrm{1}\right)\left(\mathrm{x}+\mathrm{2}\right)\left(\mathrm{1}−\mathrm{x}\right)\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}\left(\mathrm{x}+\mathrm{3}\right)\left(\mathrm{x}−\mathrm{2}\right)}\:\leqslant\:\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{we}\:\mathrm{get}\:\mathrm{solution}\:\mathrm{x}\:>\:\mathrm{2} \\ $$$$\mathrm{case}\left(\mathrm{2}\right)\:\mathrm{for}\:\mathrm{x}\leqslant−\mathrm{2}\:\cup\:\frac{\mathrm{1}}{\mathrm{2}}\leqslant\mathrm{x}<\mathrm{2} \\ $$$$\Rightarrow\frac{\left(\mathrm{2x}−\mathrm{1}\right)\left(\mathrm{x}+\mathrm{2}\right)\left(\mathrm{1}−\mathrm{x}\right)\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}\left(\mathrm{x}+\mathrm{3}\right)\left(\mathrm{2}−\mathrm{x}\right)}\:\leqslant\:\mathrm{0} \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{solution}\:\mathrm{x}<−\mathrm{3}\:\cup\:\mathrm{1}\leqslant\mathrm{x}<\mathrm{2} \\ $$$$\mathrm{case}\left(\mathrm{3}\right)\mathrm{for}\:−\mathrm{2}\leqslant\mathrm{x}\leqslant\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\frac{\left(\mathrm{1}−\mathrm{2x}\right)\left(\mathrm{x}+\mathrm{2}\right)\left(\mathrm{1}−\mathrm{x}\right)\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}\left(\mathrm{x}+\mathrm{3}\right)\left(\mathrm{2}−\mathrm{x}\right)}\:\leqslant\:\mathrm{0} \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{solution}\:−\mathrm{1}\leqslant\mathrm{x}<\mathrm{0} \\ $$$$\mathrm{finally}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{is}\: \\ $$$$\mathrm{x}>\mathrm{2}\:\cup\:\mathrm{x}<−\mathrm{3}\:\cup\mathrm{1}\leqslant\mathrm{x}<\mathrm{2}\:\cup\:−\mathrm{1}\leqslant\mathrm{x}<\mathrm{0}\: \\ $$$$\mathrm{or}\:\mathrm{x}<−\mathrm{3}\:\cup\:−\mathrm{1}\leqslant\mathrm{x}<\mathrm{0}\:\cup\:\mathrm{x}\geqslant\mathrm{1}\:;\:\mathrm{x}\neq\mathrm{2}\: \\ $$$$\:\left(−\infty,−\mathrm{3}\right)\:\cup\:\left[−\mathrm{1},\mathrm{0}\:\right)\:\cup\:\left[\mathrm{1},\:\mathrm{2}\right)\:\cup\:\left(\mathrm{2},\infty\:\right) \\ $$$$ \\ $$
